题目内容
在平面直角坐标系xOy中,曲线C1的参数方程为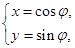 (
(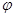 为参数)曲线C2的参数方程为
为参数)曲线C2的参数方程为 (
(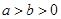 ,
,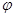 为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=
为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ= 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当 =0时,这两个交点间的距离为2,当
=0时,这两个交点间的距离为2,当 =
=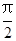 时,这两个交点重合.
时,这两个交点重合.
(I)分别说明C1,C2是什么曲线,并求出a与b的值;
(II)设当 =
= 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当 =-
=- 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
(1)a=3,b=1。
(2)四边形 的面积为
的面积为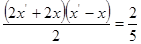
解析试题分析:(1)C1是圆,C2是椭圆
当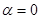 时,射线l与C1,C2的交点的直角坐标分别是(1,0)(a,0),因为两点间的距离为2,所以a=3
时,射线l与C1,C2的交点的直角坐标分别是(1,0)(a,0),因为两点间的距离为2,所以a=3
当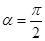 时,射线l与C1,C2的交点的直角坐标分别是(0,1)(0,b),因为两点重合,所以b=1
时,射线l与C1,C2的交点的直角坐标分别是(0,1)(0,b),因为两点重合,所以b=1
(2)C1,C2的普通方程为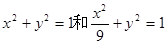

当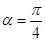 时,射线l与C1的交点
时,射线l与C1的交点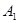 的横坐标为
的横坐标为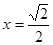 ,与
,与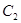 的交点
的交点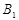 的横坐标为
的横坐标为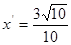
当 时,射线l与C1,C2的两个交点
时,射线l与C1,C2的两个交点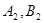 分别与
分别与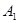 ,
,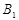 关于x轴对称,因此四边形
关于x轴对称,因此四边形 为梯形。故四边形
为梯形。故四边形 的面积为
的面积为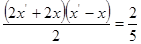
考点:极坐标方程、参数方程与直角坐标方程的互化,面积计算。
点评:中档题,利用极坐标、直角坐标转化公式。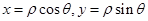 。参数方程化为普通方程,常用的“消参”方法有,代入消参、加减消参、平方关系消参等。确定四边形的面积,要注意发现其几何特征,探寻计算方法。
。参数方程化为普通方程,常用的“消参”方法有,代入消参、加减消参、平方关系消参等。确定四边形的面积,要注意发现其几何特征,探寻计算方法。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 被直线
被直线 (
( 是参数)截得的弦长.
是参数)截得的弦长. 的圆心
的圆心 ,半径
,半径
 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 两点,求弦长
两点,求弦长 的取值范围
的取值范围  经过点
经过点 ,圆心为直线
,圆心为直线 与极轴的交点,求圆
与极轴的交点,求圆 的极坐标方程是
的极坐标方程是 ,直线的参数方程是
,直线的参数方程是 (为参数).
(为参数).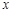 轴的交点是
轴的交点是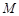 ,
, 是曲线
是曲线 的最大值.
的最大值. 经过点
经过点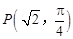 ,圆心为直线
,圆心为直线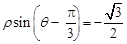 与极轴的交点,求圆
与极轴的交点,求圆 ,圆
,圆 的参数方程为
的参数方程为 (其中
(其中 为参数).
为参数). sin
sin  ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.