题目内容
求函数的值域:y=|x+1|-|2x-1|
考点:函数的值域
专题:函数的性质及应用
分析:把函数y的绝对值去掉,化为分段函数,求出每一段上的函数值域,再求它们的并集即可.
解答:
解:当x≤-1时,y=-(x+1)+(2x-1)=x-2,
∴y≤-3;
当-1<x<
时,y=(x+1)+(2x-1)=3x,
∴-3<y<
;
当x≥
时,y=(x+1)-(2x-1)=-x+2,
∴y≤
;
∴函数y=
的值域是
(-∞,-3]∪(-3,
)∪(-∞,
]=(-∞,
];
即函数y的值域是(-∞,
].
∴y≤-3;
当-1<x<
| 1 |
| 2 |
∴-3<y<
| 3 |
| 2 |
当x≥
| 1 |
| 2 |
∴y≤
| 3 |
| 2 |
∴函数y=
|
(-∞,-3]∪(-3,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
即函数y的值域是(-∞,
| 3 |
| 2 |
点评:本题考查了求含有绝对值的值域问题,解题时通常把绝对值去掉,化为分段函数解答,是基础题.

练习册系列答案
相关题目
执行如图所示的程序框图,若输入n的值为4,则输出s的值是( )


| A、2 | B、6 | C、24 | D、120 |
 如图,已知焦点在x轴上的椭圆
如图,已知焦点在x轴上的椭圆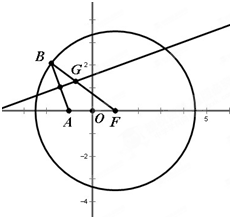 已知:定点A(-1,0),点B是⊙F:(x-1)2+y2=8(F为圆心)上的动点,线段AB的垂直平分线交BF于点G,记点G的轨迹为曲线E.
已知:定点A(-1,0),点B是⊙F:(x-1)2+y2=8(F为圆心)上的动点,线段AB的垂直平分线交BF于点G,记点G的轨迹为曲线E.