题目内容
【题目】如图,在平面直角坐标系内,已知点![]() ,
,![]() ,圆C的方程为
,圆C的方程为![]() ,点P为圆上的动点.
,点P为圆上的动点.
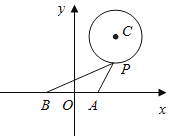
![]() 求过点A的圆C的切线方程.
求过点A的圆C的切线方程.
![]() 求
求![]() 的最大值及此时对应的点P的坐标.
的最大值及此时对应的点P的坐标.
【答案】(1)![]() 或
或![]() ;(2)最大值为
;(2)最大值为![]() ,
,![]() .
.
【解析】
![]() 分类讨论,利用点到直线的距离等于半径,即可求过点A的圆的切线的方程;
分类讨论,利用点到直线的距离等于半径,即可求过点A的圆的切线的方程;
![]() 设
设![]() ,利用两点间的距离公式表示出
,利用两点间的距离公式表示出![]() ,
,![]() ,代入所求式子中化简,整理后得出所求式子最大即为
,代入所求式子中化简,整理后得出所求式子最大即为![]() 最大,而P为圆上的点,连接OC延长与圆的交点即为此时的P点,
最大,而P为圆上的点,连接OC延长与圆的交点即为此时的P点,![]() ,求出
,求出![]() 的最大值,即可确定出所求式子的最大值.
的最大值,即可确定出所求式子的最大值.
![]() 当k存在时,设过点A切线的方程为
当k存在时,设过点A切线的方程为![]() ,
,
![]() 圆心坐标为
圆心坐标为![]() ,半径
,半径![]() ,
,
![]() ,
,
解得![]() ,
,
![]() 所求的切线方程为
所求的切线方程为![]() ,
,
当k不存在时方程![]() 也满足;
也满足;
综上所述,所求的直线方程为:![]() 或
或![]() ;
;
![]() 设点
设点![]() ,则由两点之间的距离公式知
,则由两点之间的距离公式知![]() ,
,
要![]() 取得最大值只要使
取得最大值只要使![]() 最大即可,
最大即可,
又P为圆上的点,![]() ,
,
![]() ,
,
此时直线OC:![]() ,由
,由![]() ,
,
解得![]() 舍去
舍去![]() 或
或![]() ,
,
![]() 点P的坐标为
点P的坐标为![]()

练习册系列答案
相关题目
【题目】随着互联网的发展,移动支付![]() 又称手机支付
又称手机支付![]() 逐渐深入人民群众的生活
逐渐深入人民群众的生活![]() 某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对
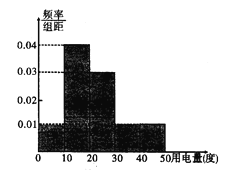
某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对![]() 岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表
岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表![]() 部分数据模糊不清
部分数据模糊不清![]() 如表:
如表:
分组 | 频数 | 频率 | |
第1组 |
| 10 |
|
第2组 |
|
|
|
第3组 |
| 15 |
|
第4组 |
|
|
|
第5组 |
| 2 |
|
合计 | 50 |
| |
![]() 表中
表中![]() 处的数据分别是多少?
处的数据分别是多少?
![]() 从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
![]() 在
在![]() 抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.