题目内容
(1)求过点A(2,4)向圆x2+y2=4所引的切线方程
(2)求直线
x+y-2
=0截圆x2+y2=4得的劣弧所对的圆心角.
(2)求直线
| 3 |
| 3 |
考点:直线与圆相交的性质,圆的切线方程
专题:直线与圆
分析:(1)根据直线和圆相切的等价条件即可求出圆x2+y2=4的切线方程.
(2)根据直线和圆相交的性质即可得到结论.
(2)根据直线和圆相交的性质即可得到结论.
解答:
解:(1)当直线斜率不存在时,直线方程为x=2,满足条件;
若直线斜率存在设斜率为k,则切线方程为y-4=k(x-2),即kx-y+4-2k=0,
由圆心到直线的距离d=2得
=2,
解得k=
,即切线方程为3x-4y+10=0,
故切线方程为x=2或3x-4y+10=0.
(2)因为直线
x+y-2
=0的斜率k=-
,
所以直线的倾斜角为120°,故弦、两半径围成一个等边三角形
所以所求的角为
.
若直线斜率存在设斜率为k,则切线方程为y-4=k(x-2),即kx-y+4-2k=0,
由圆心到直线的距离d=2得
| |4-2k| | ||
|
解得k=
| 3 |
| 4 |
故切线方程为x=2或3x-4y+10=0.
(2)因为直线
| 3 |
| 3 |
| 3 |
所以直线的倾斜角为120°,故弦、两半径围成一个等边三角形
所以所求的角为
| π |
| 3 |
点评:本题主要考查直线和圆相切和相交的应用,根据圆心和直线的距离和半径之间的关系是解决本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 正方体ABCD-A1B1C1D1的棱长为1,底面ABCD内任一点M,作MN⊥BC,垂足为N,满足条件|A1M|2-|MN|2=1.则点M的轨迹为( )
正方体ABCD-A1B1C1D1的棱长为1,底面ABCD内任一点M,作MN⊥BC,垂足为N,满足条件|A1M|2-|MN|2=1.则点M的轨迹为( )| A、线段 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
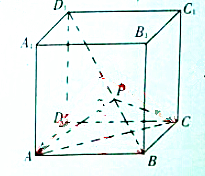
如图,已知正方体ABCD-A1B1C1D1棱长为1,点P在线段BD1上,当∠APC最大时,三棱锥P-ABC的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=sinx-a,x∈[
,
]有且仅有一个零点,则实数a的取值范围是( )
| π |
| 3 |
| 7π |
| 6 |
A、[-
| ||||||
B、[-
| ||||||
C、-
| ||||||
D、-
|
点M(1,1),点N(4,5),则|MN|=( )
| A、1 | B、2 | C、3 | D、5 |
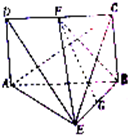 如图,已知四棱锥E-ABCD的底面ABCD是平行四边形,AE⊥BE,平面ACE⊥平面BCE,
如图,已知四棱锥E-ABCD的底面ABCD是平行四边形,AE⊥BE,平面ACE⊥平面BCE,