题目内容
函数f(x)=sinx-a,x∈[
,
]有且仅有一个零点,则实数a的取值范围是( )
| π |
| 3 |
| 7π |
| 6 |
A、[-
| ||||||
B、[-
| ||||||
C、-
| ||||||
D、-
|
考点:正弦函数的图象
专题:函数的性质及应用,三角函数的图像与性质
分析:由f(x)=sinx-a=0得sinx=a,求出函数在y=sinx在x∈[
,
]上的值域即可.
| π |
| 3 |
| 7π |
| 6 |
解答:
解:由f(x)=sinx-a=0得sinx=a,
当x∈[
,
],作出函数f(x)=sinx的图象,
由图象可知当sin
≤sinx<sin
或sinx=1时
即-
≤sinx<
,或sinx=1时
函数y=sinx和直线y=a有且仅有一个零点,
故-
≤a<
或a=1,
故选:C
当x∈[
| π |
| 3 |
| 7π |
| 6 |

由图象可知当sin
| 7π |
| 6 |
| 2π |
| 3 |
即-
| 1 |
| 2 |
| ||
| 2 |
函数y=sinx和直线y=a有且仅有一个零点,
故-
| 1 |
| 2 |
| ||
| 2 |
故选:C
点评:本题主要考查函数零点的应用,利用函数和方程之间的关系,了利用数形结合是解决本题的关键.

练习册系列答案
相关题目
计算cos300°的值( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
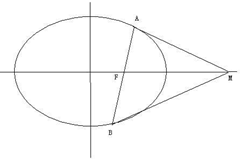 如图,椭圆
如图,椭圆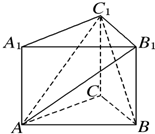 如图所示,已知三棱柱ABC A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则
如图所示,已知三棱柱ABC A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则