题目内容
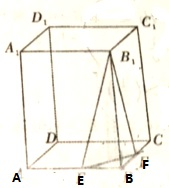
 正方体ABCD-A1B1C1D1的棱长为1,底面ABCD内任一点M,作MN⊥BC,垂足为N,满足条件|A1M|2-|MN|2=1.则点M的轨迹为( )
正方体ABCD-A1B1C1D1的棱长为1,底面ABCD内任一点M,作MN⊥BC,垂足为N,满足条件|A1M|2-|MN|2=1.则点M的轨迹为( )| A、线段 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:|A1M|2-|MN|2=1,可得|AM|=|MN|,结合MN⊥BC,由抛物线的定义,可得点M的轨迹.
解答:
解:∵|A1M|2-|MN|2=1,
∴|AM|=|MN|,
∵MN⊥BC,
∴由抛物线的定义,可得点M的轨迹为抛物线的一部分.
故选:D.
∴|AM|=|MN|,
∵MN⊥BC,
∴由抛物线的定义,可得点M的轨迹为抛物线的一部分.
故选:D.
点评:本题考查轨迹方程,考查抛物线的定义,比较基础.

练习册系列答案
相关题目
设a=tan35°,b=cos55°,c=sin23°,则( )
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、c>a>b |
 已知正四棱柱ABCD-A1B1C1D1,其底面边长为4,高为
已知正四棱柱ABCD-A1B1C1D1,其底面边长为4,高为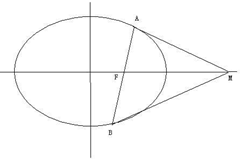 如图,椭圆
如图,椭圆