题目内容
19.若Sn为数列{an}的前n项和,且2Sn=an+1an,a1=4,则数列{an}的通项公式为an=$\left\{\begin{array}{l}{n+3,n为奇数}\\{n,n为偶数}\end{array}\right.$.分析 2Sn=an+1an,a1=4,n=1时,2×4=4a2,解得a2.n≥2时,2Sn-1=anan-1,可得2an=an+1an-anan-1,可得an+1-an-1=2.n≥2时,an+1-an-1=2,可得数列{an}的奇数项与偶数项分别为等差数列.
解答 解:∵2Sn=an+1an,a1=4,
∴n=1时,2×4=4a2,解得a2=2.
n≥2时,2Sn-1=anan-1,可得2an=an+1an-anan-1,
∴an=0(舍去),或an+1-an-1=2.
n≥2时,an+1-an-1=2,可得数列{an}的奇数项与偶数项分别为等差数列.
∴a2k-1=4+2(k-1)=2k+2.k∈N*.
a2k=2+2(k-1)=2k.
∴an=$\left\{\begin{array}{l}{n+3,n为奇数}\\{n,n为偶数}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{n+3,n为奇数}\\{n,n为偶数}\end{array}\right.$.
点评 本题考查了数列递推关系、等差数列的定义通项公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.一圆的面积以10πcm2/s速度增加,那么当圆半径r=20cm时,其半径r的增加速率u为( )
| A. | $\frac{1}{2}$cm/s | B. | $\frac{1}{3}$cm/s | C. | $\frac{1}{4}$cm/s | D. | $\frac{1}{5}$cm/s |
11.下列四个结论中正确的个数为( )
①两条不同的直线都和同一个平面平行,则这两条直线平行.
②两条不同直线都和第三条直线垂直,则这两条直线平行.
③若a∥α,b⊆α,则a∥b
④若a∥b,b⊆α,则a∥α
①两条不同的直线都和同一个平面平行,则这两条直线平行.
②两条不同直线都和第三条直线垂直,则这两条直线平行.
③若a∥α,b⊆α,则a∥b
④若a∥b,b⊆α,则a∥α
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
9.设集合A={x|x2+3x-4>0},集合B={x|-2<x≤3},且M=A∩B,则有( )
| A. | 1∈M | B. | 0∈M | C. | 1∈M | D. | 2∈M |
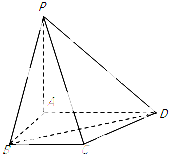 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.