题目内容
已知向量
=(4cos(
x+
),sinx),
=(sin(
x+
),sinx),定义函数f(x)=
•
+cos2x.若f(α)=2,且14≤α≤18,则tan(απ)的值为( )
| a |
| π |
| 16 |
| π |
| 8 |
| b |
| π |
| 16 |
| π |
| 8 |
| a |
| b |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积运算和倍角公式、平方关系可得函数f(x)=2sin(
x+
)+1.再利用f(α)=2,且14≤α≤18,及其诱导公式即可得出.
| π |
| 8 |
| π |
| 4 |
解答:
解:函数f(x)=
•
+cos2x=4cos(
x+
)sin(
x+
)+sin2x+cos2x=2sin(
x+
)+1,
∵f(α)=2,∴2sin(
α+
)+1=2,化为sin(
α+
)=
.
∵14≤α≤18,∴2π≤
α+
≤2π+
.
∴
α+
=2π+
,解得α=
.
∴tan(απ)=tan
=tan(15π+
)=tan
=
.
故选:A.
| a |
| b |
| π |
| 16 |
| π |
| 8 |
| π |
| 16 |
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
∵f(α)=2,∴2sin(
| π |
| 8 |
| π |
| 4 |
| π |
| 8 |
| π |
| 4 |
| 1 |
| 2 |
∵14≤α≤18,∴2π≤
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
∴
| π |
| 8 |
| π |
| 4 |
| π |
| 6 |
| 46 |
| 3 |
∴tan(απ)=tan
| 46π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
故选:A.
点评:本题考查了数量积运算、倍角公式、平方关系、诱导公式等基础知识,考查了计算能力,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
下列命题正确的是( )
(1)如果一个平面内有两条直线平行于另一个平面,那么这两个平面平行;
(2)如果一个平面内有无数条直线平行于两一个平面,那么这两个平面平行;
(3)如果一个平面内有两条相交直线,分别平行于另一个平面内的两条直线,那么这两个平面平行;
(4)如果一个平面内一个角(锐角或钝角)的两边和另一个平面内的一个角的两边分别平行,那么这两个平面平行.
(1)如果一个平面内有两条直线平行于另一个平面,那么这两个平面平行;
(2)如果一个平面内有无数条直线平行于两一个平面,那么这两个平面平行;
(3)如果一个平面内有两条相交直线,分别平行于另一个平面内的两条直线,那么这两个平面平行;
(4)如果一个平面内一个角(锐角或钝角)的两边和另一个平面内的一个角的两边分别平行,那么这两个平面平行.
| A、只有(1)(2)(4) |
| B、只有(2)(3)(4) |
| C、只有(3)(4) |
| D、四个命题都不正确 |
若f(x)=ax3+bx2+cx+d(a>0),则函数f(x)在R上为增函数的充要条件为( )
| A、b2<3ac |
| B、b2>3ac |
| C、b2≤3ac |
| D、b2≥3ac |
已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的( )
| A、充要条件 |
| B、充分不必要 |
| C、既不充分也不必要 |
| D、必要不充分 |
甲、乙、丙三人值周一至周六的班,每人值两天班,若甲不值周一、乙不值周六,则可排出不同的值班表数为( )
| A、30 | B、42 | C、48 | D、60 |
若x<0,则 x+
的最大值为( )
| 1 |
| x |
| A、-4 | B、-3 | C、-2 | D、-1 |

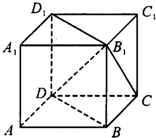 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中,