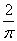题目内容
已知函数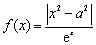 ,其中
,其中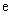 是自然对数的底数,实数
是自然对数的底数,实数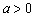 .
.
(1)试求函数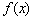 的单调区间;
的单调区间;
(2)证明:函数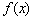 的极值点
的极值点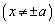 与原点连线的斜率之乘积为定值.
与原点连线的斜率之乘积为定值.
解析:(1)
①当
令
∵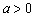 ,∴
,∴
∴当
当
②当
同①可知当 ,当
,当
∴函数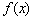 的单调递增区间为
的单调递增区间为 ,
,
单调递减区间为


法二、先求 ,
,
令
 ,
,
当 时,
时, ,当
,当 时,
时,
∴ 在
在 和
和 上单调递减,在
上单调递减,在 上单调递增
上单调递增
将 图象在
图象在 轴下方的图象沿
轴下方的图象沿 轴翻折到
轴翻折到 轴上方连同
轴上方连同 图象原来在
图象原来在 轴上方的图象得到
轴上方的图象得到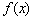 的图象
的图象
又 ,
,  ,及
,及 时,
时,
∴函数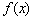 的单调递增区间为
的单调递增区间为 ,
,
单调递减区间为


(2)由(1)可知当 时,函数
时,函数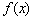 取极大值,
取极大值,
且
可知当 时,函数
时,函数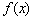 取极大值,
取极大值,
且
∴ ,
,


∴ 为定值.
为定值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 过点
过点 且垂直于直线
且垂直于直线 ,则直线
,则直线 展开式的常数项是
展开式的常数项是 ,则常数
,则常数 的值为 .
的值为 . 展开式中
展开式中 的系数为80,则实数a的值为________.
的系数为80,则实数a的值为________.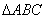 中,角
中,角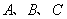 所对的边分别为
所对的边分别为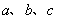 ,且满足
,且满足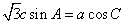
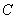 的大小;
的大小;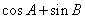 的取值范围.
的取值范围. 的不等式
的不等式 对于一切实数
对于一切实数 ” 的
” 的 与双曲线
与双曲线 ,有如下信息:联立方程组:
,有如下信息:联立方程组: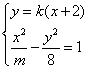 , 消去
, 消去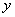 后得到方程
后得到方程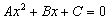 ,分类讨论:(1)当
,分类讨论:(1)当 时,
时,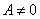 时,
时,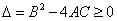 恒成立。在满足所提供信息
恒成立。在满足所提供信息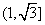 B.
B.
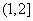 D.
D.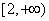
 是等比数列,前
是等比数列,前 项和为
项和为 ,
, ,则
,则
 B.
B. 
 D.
D. 
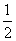 ,则周末去踢球,否则去图书馆.则小波周末去图书馆的概率是
,则周末去踢球,否则去图书馆.则小波周末去图书馆的概率是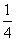 B.
B. 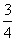 C.
C.