题目内容
9.已知圆M:(x-a)2+y2=4(a>0)与圆N:x2+(y-1)2=1外切,则直线x-y-$\sqrt{2}$=0被圆M截得线段的长度为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 利用圆M:(x-a)2+y2=4(a>0)与圆N:x2+(y-1)2=1外切,求出a,可得圆心M(2$\sqrt{2}$,0)到直线x-y-$\sqrt{2}$=0的距离,即可求出直线x-y-$\sqrt{2}$=0被圆M截得线段的长度.
解答 解:由题意,$\sqrt{{a}^{2}+1}$=2+1,∴a=2$\sqrt{2}$,
圆心M(2$\sqrt{2}$,0)到直线x-y-$\sqrt{2}$=0的距离d=$\frac{|2\sqrt{2}-0-\sqrt{2}|}{\sqrt{2}}$=1,
∴直线x-y-$\sqrt{2}$=0被圆M截得线段的长度为2$\sqrt{4-1}$=2$\sqrt{3}$,
故选D.
点评 本题考查圆与圆的位置关系,考查直线与圆的位置关系,考查点到直线的距离公式,属于中档题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
20.已知集合A={1,2,3},B={x|x2-3x+a=0,a∈A},若A∩B≠∅,则a的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 1或2 |
4.有以下两个推理过程:
(1)在等差数列{an}中,若a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立.相应地,在等比数列{bn}中,若b10=1,则有等式b1b2…bn=b1b2…b19-n(n<19,n∈N*);
(2)由1=12,1+3=22,1+3+5=32,1+3+5+…+(2n-1)=n2.
则(1)(2)两个推理过程分别属于( )
(1)在等差数列{an}中,若a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立.相应地,在等比数列{bn}中,若b10=1,则有等式b1b2…bn=b1b2…b19-n(n<19,n∈N*);
(2)由1=12,1+3=22,1+3+5=32,1+3+5+…+(2n-1)=n2.
则(1)(2)两个推理过程分别属于( )
| A. | 归纳推理、演绎推理 | B. | 类比推理、演绎推理 | ||
| C. | 归纳推理、类比推理 | D. | 类比推理、归纳推理 |
18.用二分法研究函数f(x)=x3-2x-1的理念时,若零点所在的初始区间为(1,2),则下一个有解区间为( )
| A. | (1,2) | B. | (1.75,2) | C. | (1.5,2) | D. | (1,1.5) |
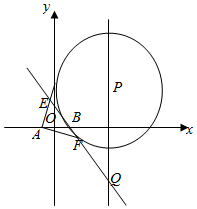 如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.
如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.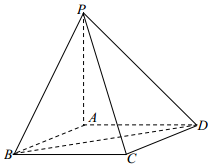 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PB=PC=PD.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PB=PC=PD.