题目内容
20.以椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的中心为顶点,左焦点为焦点的抛物线的标准方程是( )| A. | x2=8y | B. | y2=16x | C. | x2=-8y | D. | y2=-16x |
分析 求出椭圆的a,b,c,可得左焦点,即可得到开口向左的抛物线的方程.
解答 解:椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的a=5,b=3,
c=$\sqrt{{a}^{2}-{b}^{2}}$=4,
可得左焦点为(-4,0),
即有抛物线的方程为y2=-16x.
故选:D.
点评 本题考查椭圆的方程和性质,以及抛物线的方程的求法,考查运算能力,属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
16.已知函数f(x)=(x-$\frac{1}{x}$)•sinx,x∈[-π,π]且x≠0,下列描述正确的是( )
| A. | 函数f(x)为奇函数 | B. | 函数f(x)既无最大值也无最小值 | ||
| C. | 函数f(x)有4个零点 | D. | 函数f(x)在(0,π)单调递增 |
10.执行如图所示的程序框图,则输出的结果是( )
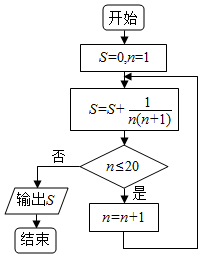

| A. | $\frac{22}{23}$ | B. | $\frac{21}{22}$ | C. | $\frac{20}{21}$ | D. | $\frac{19}{20}$ |