题目内容
9.已知A(x1,0),B(x2,1)在函数f(x)=2sin(ωx+φ)(ω>0)的图象上,|x1-x2|的最小值为$\frac{π}{4}$,则ω=$\frac{2}{3}$.分析 根据已知可得函数的周期T=3π,进而可得答案.
解答 解:∵A(x1,0),B(x2,1)在函数f(x)=2sin(ωx+φ)(ω>0)的图象上,|x1-x2|的最小值为$\frac{π}{4}$,由B点坐标可知|AB|的距离最小为$\frac{π}{6}$
故$\frac{π}{4}$=$\frac{T}{12}$,
解得:T=3π,
又由ω>0,
故ω=$\frac{2π}{T}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查的知识点是正弦函数的图象和性质,熟练掌握正弦函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
20.下列判断中错误的是( )
| A. | 角α确定时,它在单位圆中的正弦线确定 | |
| B. | 单位圆中有相同正弦线的角相等 | |
| C. | 角α和角α+π具有相同的正切线 | |
| D. | 单位圆中有相同正切线的角的终边在同一直线上 |
1.已知α=9 rad,β=10 rad,下面关于α和β的说法正确的是( )
| A. | 都是第一象限角 | B. | 都是第二象限角 | ||
| C. | 分别是第二象限和第三象限的角 | D. | 分别是第三象限和第四象限的角 |
18.执行如下图的程序框图,则输出的数是( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.若函数f(x)=2exln(x+m)+ex-2存在正的零点,则实数m的取值范围( )
| A. | (-∞,$\sqrt{e}$) | B. | ($\sqrt{e}$,+∞) | C. | (-∞,e) | D. | (e,+∞) |
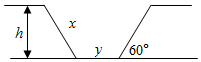 某地兴修水利开建一条水渠,其断面为等腰梯形,腰与水平线的夹角为60°,要求湿透周长(即断面与水接触的边界长度)为定值l.问渠深h为多少时,可使水流量最大?最大水流量是多少?
某地兴修水利开建一条水渠,其断面为等腰梯形,腰与水平线的夹角为60°,要求湿透周长(即断面与水接触的边界长度)为定值l.问渠深h为多少时,可使水流量最大?最大水流量是多少?