题目内容
9.已知函数f(x)=x2-ax+a.设p:方程f(x)=0有实数根;q:函数f(x)在区间[1,2]上是增函数.若p或q为真命题,p且q为假命题,求实数a的取值范围.分析 首先考虑命题p,q均为真命题,求出a的取值范围,再根据p,q中一真一假,分别求出a的取值范围,最后求并集.
解答 解:若p真,即方程f(x)=0有实数根,
则△=a2-4a≥0?a≤0,或a≥4;…(2分)
若q真,即函数f(x)在区间[1,2]上是增函数,
则区间[1,2]在对称轴的右边即$\frac{a}{2}$≤1⇒a≤2…(3分)
因为p和q有且只有一个正确,所以p,q中一真一假.
若p真q假,则 $\left\{\begin{array}{l}{a≤0或a≥4}\\{a>2}\end{array}\right.$⇒a≥4;
若p假q真,则 $\left\{\begin{array}{l}{0<a<4}\\{a≤2}\end{array}\right.$⇒0<a≤2.…(7分)
所以实数a的取值范围为(0,2]∪[4,+∞).
点评 本题主要考查命题的真假判断和应用,同时考查函数的单调性和集合、不等式的运算,是一道基础题.

练习册系列答案
相关题目
17.实数x,y满足约束条件$\left\{\begin{array}{l}x+y≤4\\ 3x-y≥0\\ y≥0\end{array}\right.$,则目标函数z=2x-y的最小值为( )
| A. | -1 | B. | 2 | C. | 4 | D. | 8 |
18.某县二中有教职员工300人,不到35岁的有140人,35岁到50岁的有110人,剩下的为51岁以上的人,用分层抽样的方法从中抽取30人,各年龄段分别抽取多少人( )
| A. | 13,11,6 | B. | 14,11,5 | C. | 15,11,4 | D. | 16,11,3 |
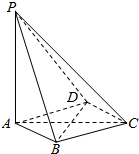 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.