题目内容
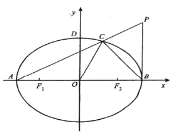
【题目】已知抛物线![]() :
:![]() ,焦点为
,焦点为![]() ,其准线与
,其准线与![]() 轴交于点
轴交于点![]() .椭圆
.椭圆![]() :分别以
:分别以![]() 、
、![]() 为左、右焦点,其离心率
为左、右焦点,其离心率![]() ,且抛物线
,且抛物线![]() 和椭圆
和椭圆![]() 的一个交点记为
的一个交点记为![]() .
.
(1)当![]() 时,求椭圆
时,求椭圆![]() 的标准方程;
的标准方程;
(2)在(1)的条件下,若直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,且与抛物线
,且与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,若弦长
两点,若弦长![]() 等于
等于![]() 的周长,求直线
的周长,求直线![]() 的方程.
的方程.
【答案】(1)![]() =1
=1
(2)![]()
【解析】
(1)当![]() 时,F
时,F![]() (1,0),F
(1,0),F![]() (-1,0) 设椭圆
(-1,0) 设椭圆![]() 的标准方程为
的标准方程为![]() (
(![]() >
>![]() >0),
>0),
∴![]() =1,
=1,![]() =
=![]() ∵
∵![]() ,∴
,∴![]() =2,
=2,![]() =
=![]()
故椭圆![]() 的标准方程为
的标准方程为![]() =1.
=1.
(2) (ⅰ)若直线![]() 的斜率不存在,则
的斜率不存在,则![]() :
:![]() =1,且A(1,2),B(1,-2),∴
=1,且A(1,2),B(1,-2),∴![]() =4
=4
又∵![]() 的周长等于
的周长等于![]() =2
=2![]() +2
+2![]() =6
=6![]()
![]()
∴直线![]() 的斜率必存在.
的斜率必存在.
ⅱ)设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() :
:![]() 由
由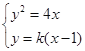 ,得
,得![]()
∵直线![]() 与抛物线
与抛物线![]() 有两个交点A,B,
有两个交点A,B,
∴![]() ,且
,且![]()
设![]()
则可得![]() ,
,![]() .
.
于是![]() =
=![]() =
=![]()
=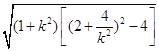
=![]()
=![]() .
.
∵![]() 的周长等于
的周长等于![]() =2
=2![]() +2
+2![]() =6.
=6.
∴由![]() =6,解得
=6,解得![]() =
=![]() .
.
故所求直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
相关题目