Question

【题目】已知二次函数f（x）满足条件f（0）＝1，及f（x+1）﹣f（x）＝2x．

（1）求函数f（x）的解析式；

（2）在区间[﹣1，1]上，y＝f（x）的图象恒在y＝2x+m的图象上方，试确定实数m的取值范围．

Answer 1

【答案】（1）（2）m＜﹣1

【解析】

（1）根据二次函数f（x）满足条件f（0）＝1，及f（x+1）﹣f（x）＝2x，可求f（1）＝1，f（﹣1）＝3，从而可求函数f（x）的解析式；

（2）在区间[﹣1，1]上，y＝f（x）的图象恒在y＝2x+m的图象上方，等价于x2﹣x+1＞2x+m在[﹣1，1]上恒成立，等价于x2﹣3x+1＞m在[﹣1，1]上恒成立，求出左边函数的最小值，即可求得实数m的取值范围．

解：（1）令x＝0，则∵f（x+1）﹣f（x）＝2x，

∴f（1）﹣f（0）＝0，

∴f（1）＝f（0）

∵f（0）＝1

∴f（1）＝1，

∴二次函数图象的对称轴为．

∴可令二次函数的解析式为f（x）．

令x＝﹣1，则∵f（x+1）﹣f（x）＝2x，

∴f（0）﹣f（﹣1）＝﹣2

∵f（0）＝1

∴f（﹣1）＝3，

∴

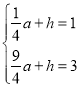
∴a＝1，

∴二次函数的解析式为

（2）∵在区间[﹣1，1]上，y＝f（x）的图象恒在y＝2x+m的图象上方

∴x2﹣x+1＞2x+m在[﹣1，1]上恒成立

∴x2﹣3x+1＞m在[﹣1，1]上恒成立

令g（x）＝x2﹣3x+1，则g（x）＝（x）2

∴g（x）＝x2﹣3x+1在[﹣1，1]上单调递减，

∴g（x）min＝g（1）＝﹣1，

∴m＜﹣1.