题目内容
【题目】已知函数
是定义域为
的奇函数，当
时，
．
（
）求出函数在上的解析式；
（
）画出函数的图象，并根据图象直接写出的单调区间；
（
）求使
时的
的值．
【答案】（
）
；（
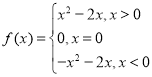）图象见解析，
的单调增区间是
和
，单调减区间是
；（
）
或
．
【解析】
设
则
,根据函数为奇函数,
，当
时, 
,可得解析式;当
时有
;即得函数在
上解析式.
根据当时，,利用描点法画出当时的图象,再利用奇函数的图象关于原点对称,可得当
时,的图象;时,;即得的图象;利用图象可得函数的单调区间.
由知,结合
的范围,分两种情况解方程即可得的值.
（）当时，
，
．
∵是定义在上的奇函数，
∴
，且当时，
，
∴
．
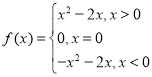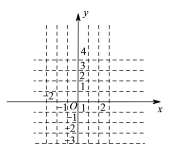
（）图象如图所示：
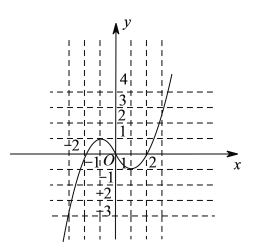
的单调增区间是和，单调减区间是．
（）当时，
等价于
，解得
或
（舍去），
当时，等价于
，解得
．
综上所述，的值为或．
练习册系列答案
阅读快车系列答案
相关题目
