题目内容
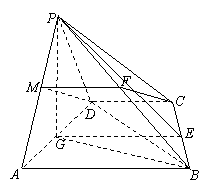
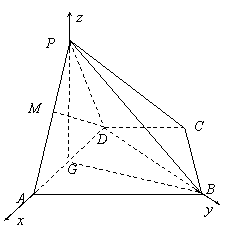
如图,四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,
, ,侧面
,侧面 底面
底面 ,且
,且 为等腰直角三角形,
为等腰直角三角形, ,
, 为
为 的中点.
的中点.
 (Ⅰ)求证:
(Ⅰ)求证: ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的正切值.
的正切值.
【解】 解法一:(Ⅰ)取 的中点
的中点 ,连结
,连结 . ……1分
. ……1分
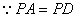 ,
, 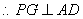 .
.
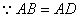 ,且
,且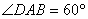 ,
,
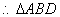 是正三角形,
是正三角形,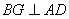 .
.
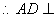 平面
平面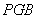 .
.
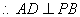 .
.
(Ⅱ)取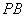 的中点
的中点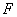 ,联结
,联结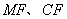 ,
,
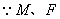 分别为
分别为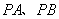 的中点,
的中点,
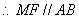 ,且
,且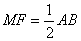 . 分
. 分
∵四边形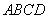 是直角梯形,
是直角梯形,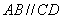 且
且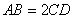 ,
,
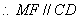 且
且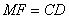 . ∴四边形
. ∴四边形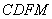 是平行四边形.
是平行四边形.
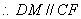 .
.
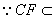 平面
平面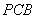 ,
,
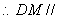
平面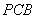 .
.
(Ⅲ)取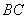 的中点
的中点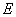 ,联结
,联结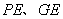 .
.
∵四边形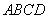 是直角梯形且
是直角梯形且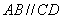 ,
,
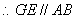 ,
,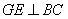 .
.
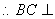 平面
平面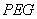 ,
,
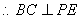 ,
,
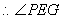 是二面角
是二面角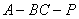 的平面角. 设
的平面角. 设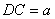 ,则
,则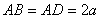 .
.
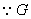 、
、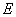 分别为
分别为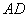 、
、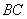 中点,
中点,
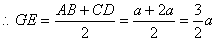 .
.
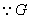 是等腰直角三角形
是等腰直角三角形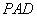 斜边的中点,
斜边的中点,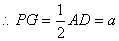 .
. 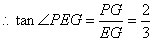 ,
,
∴二面角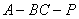 的正切值为
的正切值为 . 解法二:(Ⅰ)同解法1
. 解法二:(Ⅰ)同解法1
(Ⅱ) ∵侧面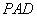
 底面
底面 ,
,
又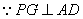 ,
, 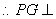 底面
底面 .
.
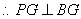 .
.
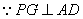 .
.
∴直线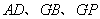 两两互相垂直,故可以分别以直线
两两互相垂直,故可以分别以直线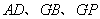 为
为 轴、
轴、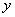 轴和
轴和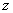 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系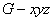 . 设
. 设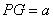 ,
,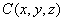 ,则可求得
,则可求得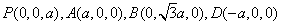 ,则
,则
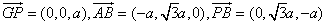 .
. 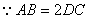 且
且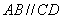 ,
,
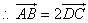 ,即
,即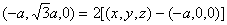 .
.
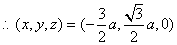 ,即
,即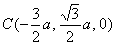 .
.
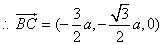 .
.
设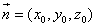 是平面
是平面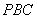 的法向量,则
的法向量,则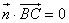 且
且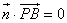 .
.
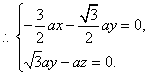
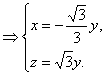
取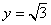 ,得
,得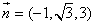 .
. 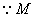 是
是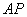 的中点,
的中点, 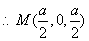 .
.
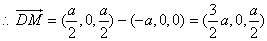 .
.
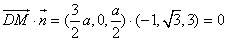 .
.
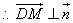 .
.
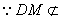 平面
平面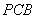 ,
,
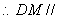 平面
平面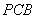 . ……
. ……
(Ⅲ)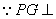 平面
平面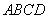 ,
,
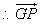 是平面
是平面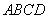 的法向量,
的法向量, 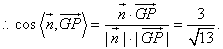 …
…
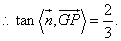
∴二面角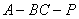 的正切值为
的正切值为 .
.
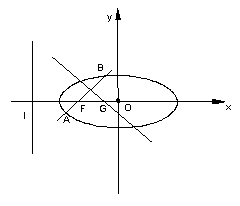

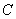 与圆
与圆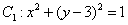 和圆
和圆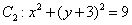 都外切,则动圆圆心
都外切,则动圆圆心 与圆C:
与圆C: 相交于A、B两点,则
相交于A、B两点,则 的值为 ___ .
的值为 ___ .  ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 是椭圆
是椭圆 上的一个动点,则
上的一个动点,则 的最大值为_______________ .
的最大值为_______________ . B.-
B.- D.-
D.- 与双曲线
与双曲线 有公共点P,则P与双曲线二焦点连线构成三角形面积为( )
有公共点P,则P与双曲线二焦点连线构成三角形面积为( )  C.5 D.3
C.5 D.3 在[0,3]上的最大值和最小值分别是( )
在[0,3]上的最大值和最小值分别是( )  C. 5,
C. 5, D. 5,
D. 5,
 ,
,
 ,则
,则 ( )
( ) B.
B.  C.
C. D.
D.