题目内容
18.正方体ABCD-A1B1C1D1中,N为BB1的中点,则直线AN与B1C所成角的余弦值是( )| A. | $\frac{\sqrt{5}}{10}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{10}}{10}$ | D. | $\frac{\sqrt{10}}{10}$ |
分析 建立空间直角坐标系,先求向量$\overrightarrow{AN}$,$\overrightarrow{{B}_{1}C}$,夹角的余弦值,可得异面直线所成角的余弦值,可得答案.
解答 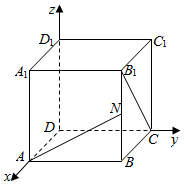 解:分别以DA、DC、DD1所在直线为x、y、z轴建立空间直角坐标系,
解:分别以DA、DC、DD1所在直线为x、y、z轴建立空间直角坐标系,
设正方体棱长为2,可得D(0,0,0),A(2,0,0),N(2,2,1),B1(2,2,2),C(0,2,0),
∴$\overrightarrow{AN}$=(0,2,1),$\overrightarrow{{B}_{1}C}$=(-2,0,-2),
∴∴cos<$\overrightarrow{AN}$,$\overrightarrow{{B}_{1}C}$>=$\frac{\overrightarrow{AN}•\overrightarrow{{B}_{1}C}}{|\overrightarrow{AN}||\overrightarrow{{B}_{1}C}|}$=-$\frac{\sqrt{10}}{10}$,
∴异面直线DE与B1C所成角的余弦值为$\frac{\sqrt{10}}{10}$,
故选:D.
点评 本题考查异面直线所成的角,建立空间直角坐标系是解决问题的关键,属中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
9.已知边长为2的正方形ABCD的四个顶点在球O的球面上,二面角O-AB-C的平面角为60°,则球O的体积为( )
| A. | $\frac{{20\sqrt{5}}}{3}π$ | B. | $\frac{{64\sqrt{2}}}{3}π$ | C. | 20π | D. | 32π |
6.已知集合A={1,2,3,4},B={0,1,3},C={3,4},那么(A∩B)∪C=( )
| A. | {3} | B. | {3,4} | C. | {1,3,4} | D. | {0,1,2,3,4} |
13.某2017年夏令营组织5名营业员参观北京大学、清华大学等五所大学,要求每人任选一所大学参观,则有且只有两个人选择北京大学的不同方案共有( )
| A. | 240种 | B. | 480种 | C. | 640种 | D. | 1280种 |
10.已知直三棱柱ABC-A1B1C1中,AB=3,BC=AA1=2,∠ABC=$\frac{π}{3}$,则异面直线B1A与C1B所成角的余弦值为( )
| A. | $\frac{\sqrt{13}}{13}$ | B. | $\frac{\sqrt{13}}{26}$ | C. | $\frac{\sqrt{13}}{52}$ | D. | $\frac{\sqrt{26}}{52}$ |
7.为确定某零件加工时间,某工人做了四次试验,得到的数据如表:
(1)若y关于x的线性回归方程为$\stackrel{∧}{y}$=1.4x+$\stackrel{∧}{a}$,求出$\stackrel{∧}{a}$的值i
(2)试预测加工8个零件需要多少时间.
| x(小时) | 2 | 3 | 4 | 5 |
| y(个) | 1 | 2 | 4 | 5 |
(2)试预测加工8个零件需要多少时间.