题目内容
19.设24<a≤25,5<b≤12.求a+b,a-b,ab,$\frac{a}{b}$的取值范围.分析 根据不等式的性质即可得到结论.
解答 解:∵24<a≤25,5<b≤12,
∴-12≤-b<-5,$\frac{1}{12}$≤$\frac{1}{b}$<$\frac{1}{5}$
则029a+b≤37,12<a-b<20,120≤ab<300,2<$\frac{a}{b}$<5.
点评 本题主要考查不等式的性质,要求熟练掌握不等式的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.设U=R,M={x|x2-2x>0},则∁RM=( )
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0]∪[2,+∞) |
4.一个空间几何体的正视图和侧视图都是边长为1的正三角形,俯视图是一个直径为1的圆,那么这个几何体的全面积为( )
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{4}$ | C. | π | D. | 2π |
15.某空间几何体的三视图及其尺寸如图所示,则该几何体的表面积是( )
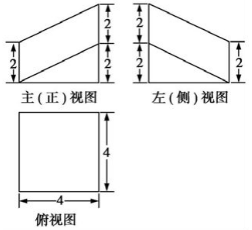

| A. | 32+8$\sqrt{6}$ | B. | 48+8$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 44+8$\sqrt{6}$ |
 已知某几何体的三视图如图所示.
已知某几何体的三视图如图所示.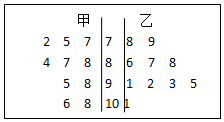 在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.
在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.