题目内容
18.已知数列{an}为等差数列,满足$\left\{\begin{array}{l}2≤{a_1}+2{a_2}≤4\\-1≤2{a_2}+3{a_3}≤1\end{array}\right.$,则当a4取最大值时,数列{an}的通项公式为an=$-\frac{1}{2}n+\frac{3}{2}$.分析 转化表达式为首项与公差的不等式组,画出约束条件的可行域,利用a4取最大值,求出首项与公差,即可求解通项公式.
解答 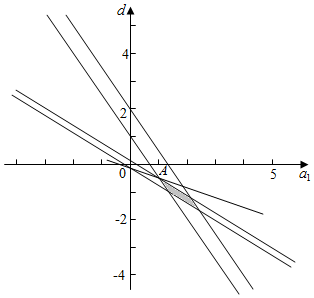 解:由题意可得:$\left\{\begin{array}{l}{2≤3{a}_{1}+2d≤4}\\{-1≤5{a}_{1}+8d≤1}\end{array}\right.$,a4=a1+3d,
解:由题意可得:$\left\{\begin{array}{l}{2≤3{a}_{1}+2d≤4}\\{-1≤5{a}_{1}+8d≤1}\end{array}\right.$,a4=a1+3d,
画出约束条件的可行域如图:
a4=a1+3d,当a4=a1+3d,经过可行域的A点时,a4取得最大值,
由$\left\{\begin{array}{l}{3{a}_{1}+2d=2}\\{5{a}_{1}+8d=1}\end{array}\right.$,可得a1=1,d=$-\frac{1}{2}$.
此时a4取最大值,an=$-\frac{1}{2}n+\frac{3}{2}$.
故答案为:$-\frac{1}{2}n+\frac{3}{2}$.
点评 本题考查线性规划的简单应用,数列的性质的应用,考查转化思想以及数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.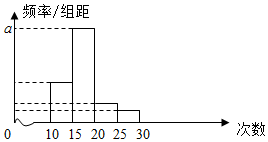 对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(1)求出表中n,p及图中a的值;
(2)估计高二年级学生参加社区服务次数的平均数和中位数(保留一位小数).
 对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
(2)估计高二年级学生参加社区服务次数的平均数和中位数(保留一位小数).
9.设A,B是函数f(x)定义域集合的两个子集,如果对任意xl∈A,都存在x2∈B,使得f(x1)f(x2)=l,则称函数f(x)为定义在集合A,B上的“倒函数”,若函数f(x)=x2-$\frac{2}{3}$ ax3(a>0),x∈R为定义在A=(2,+∞),B=(1,+∞)两个集合上的“倒函数”,则实数a取值范围是( )
| A. | (0,$\frac{3}{4}$]∪[$\frac{3}{2}$,+∞) | B. | (0,$\frac{3}{4}]$ | C. | [$\frac{3}{2}$,+∞) | D. | [$\frac{3}{4},\frac{3}{2}]$ |
3.设数列{an}中,已知a1=1,an=1+$\frac{1}{{a}_{n-1}}$(n>1),则a4=( )
| A. | $\frac{8}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
10.不等式$\frac{3x-1}{x-2}>0$的解集是( )
| A. | $\left\{{x|x<\frac{1}{3}或x>2}\right\}$ | B. | $\left\{{x|\frac{1}{3}<x<2}\right\}$ | C. | {x|x>2} | D. | $\left\{{x|x<\frac{1}{3}}\right\}$ |
8.已知△ABC是锐角三角形,则点P(cosC-sinA,sinA-cosB)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |