题目内容
6.已知函数f(x)=asin2x+bcos2x(a>b)的值域为[1,3](1)求a、b的值与f(x)的最小正周期;
(2)用五点法画出上述函数在区间[-π,π]上的大致图象.
分析 (1)根据降幂公式,化简得f(x)=$\frac{1}{2}$(b-a)cos2x+$\frac{1}{2}$(a+b),函数的值域为[1,3],列方程解得a=3,b=1,写出函数解析式,T=$\frac{2π}{ω}$;
(2)根据五点画出函数图象.
解答 解:(1)f(x)=asin2x+bcos2x(a>b),由降幂公式,可得:
f(x)=a•$\frac{1-cos2x}{2}$+b$\frac{1+cos2x}{2}$,
=$\frac{1}{2}$(b-a)cos2x+$\frac{1}{2}$(a+b),
函数f(x)的值域为[1,3],(a>b)
$\frac{1}{2}$(b-a)+$\frac{1}{2}$(a+b)=1,
-$\frac{1}{2}$(b-a)+$\frac{1}{2}$(a+b)=3,
解得:a=3,b=1,
∴f(x)=-cos2x+2,
T=$\frac{2π}{ω}$=$\frac{2π}{2}$=π,
f(x)的最小正周期π;
(2)函数在区间[-π,π]上的大致图象如图.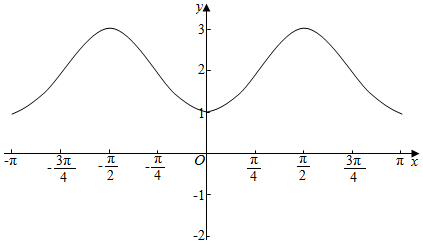
点评 本题考查降幂公式,求函数解析式,采用函数五点法,绘制函数解析式.

练习册系列答案
相关题目
16.请阅读问题1的解答过程,然后借鉴问题1的解题思路完成问题2的解答:
问题1:已知数集A={a1,a2,…an}(1≤a1<a2<…<an,n≥2)具有性质P:对任意的i,j(1≤i≤j≤n),aiaj与$\frac{a_j}{a_i}$两数中至少有一个属于A.若数集{a1,2,3,a4}具有性质P,求a1,a4的值.
问题2:已知数集A={a1,a2,…an}(0≤a1<a2<…<an,n≥2)具有性质P:
对任意的i,j(1≤i≤j≤n),ai+aj与aj-ai两数中至少有一个属于A.若数集{a1,1,3,a4}具有性质P,求a1,a4的值.
问题1:已知数集A={a1,a2,…an}(1≤a1<a2<…<an,n≥2)具有性质P:对任意的i,j(1≤i≤j≤n),aiaj与$\frac{a_j}{a_i}$两数中至少有一个属于A.若数集{a1,2,3,a4}具有性质P,求a1,a4的值.
| 解:对于集合中最大的数a4,因为a4×a4>a4,3×a4>a4,2×a4>a4. 所以$\frac{a_4}{a_4}$,$\frac{a_4}{3}$,$\frac{a_4}{2}$都属于该集合. 又因为1≤a1<2<3<a4,所以$\frac{a_4}{a_4}<\frac{a_4}{3}<\frac{a_4}{2}<{a_4}$. 所以${a_1}=\frac{a_4}{a_4}=1$,$\frac{a_4}{3}=2,\frac{a_4}{2}=3$,故a1=1,a4=6. |
对任意的i,j(1≤i≤j≤n),ai+aj与aj-ai两数中至少有一个属于A.若数集{a1,1,3,a4}具有性质P,求a1,a4的值.
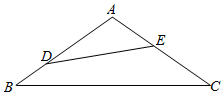 某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°
某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°