题目内容
设平面 与平面
与平面 相交于直线
相交于直线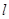 ,直线
,直线 在平面
在平面 内,直线
内,直线 在平面
在平面 内,且
内,且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
解析试题分析:因为 ,直线
,直线 在平面
在平面 内,且
内,且 ,
, ,而直线
,而直线 在平面
在平面 内,
内, ,反之
,反之 ,当
,当 时,
时, 就不一定成立.
就不一定成立.
考点:1、线面垂直的性质,2、逻辑.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
如图在棱长均为2的正四棱锥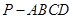 中,点
中,点 为
为 中点,则下列命题正确的是( )
中点,则下列命题正确的是( )
A.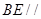 面 面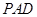 ,且直线 ,且直线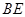 到面 到面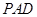 距离为 距离为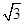 |
B.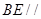 面 面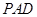 ,且直线 ,且直线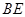 到面 到面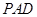 距离为 距离为 |
C.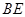 不平行于面 不平行于面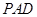 ,且 ,且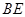 与平面 与平面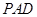 所成角大于 所成角大于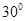 |
D.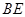 不平行于面 不平行于面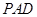 ,且 ,且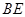 与平面 与平面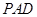 所成角小于 所成角小于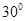 |
下列命题正确的是( )
| A.若两条直线和同一个平面所成的角相等, 则这两条直线平行; |
| B.若一个平面内有三点到另一个平面的距离相等,则这两个平面平行; |
| C.若一条直线和两个相交平面都平行, 则这条直线与这两个平面的交线平行; |
| D.若两个平面都垂直于第三个平面, 则这两个平面平行. |
在下列条件下,可判断平面α与平面β平行的是( )
| A.α、β都垂直于平面γ |
| B.α内不共线的三个点到β的距离相等 |
| C.l,m是α内两条直线且l∥β,m∥β |
| D.l,m是异面直线,且l∥α,m∥α,l∥β,m∥β |
三棱柱 中,
中,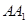 与
与 、
、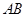 所成角均为
所成角均为 ,
, ,且
,且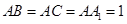 ,则
,则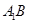 与
与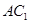 所成角的余弦值为( )
所成角的余弦值为( )
| A.1 | B.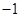 | C.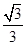 | D.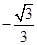 |
对于平面 、
、 、
、 和直线
和直线 、
、 、
、 、
、 ,下列命题中真命题是( )
,下列命题中真命题是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 则 则 |
D.若 ,则 ,则 |
正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为( )
| A.75° | B.60° | C.45° | D.30° |
设 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列正确的个数为:( )
是两个不同的平面,则下列正确的个数为:( )
①若 ,则
,则 ; ②若
; ②若 ,则
,则 ;
;
③若 ,则
,则 或
或 ;④若
;④若 ,则
,则
| A.1 | B.2 | C.3 | D.4 |
 ,则 M 到面 ABC 的距离为( )
,则 M 到面 ABC 的距离为( )


