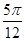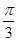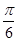题目内容
三棱柱 中,
中,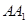 与
与 、
、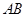 所成角均为
所成角均为 ,
, ,且
,且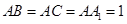 ,则
,则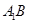 与
与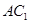 所成角的余弦值为( )
所成角的余弦值为( )
| A.1 | B.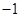 | C.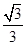 | D.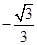 |
C
解析试题分析:将三棱柱上,下底面补成平行四边形 ,连
,连 ,则多面体
,则多面体 为 平行六面体,连接
为 平行六面体,连接 , 则
, 则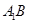 ∥
∥ ,所以相交线
,所以相交线 与
与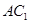 所成的锐角或直角即为异面直线
所成的锐角或直角即为异面直线 所成的角.
所成的角.
在 中,角
中,角 ,所以
,所以 ,即
,即 ;
;
在平行四边形 中,角
中,角 ,所以
,所以 ;
;
在平行四边形 中,因为
中,因为 , 所以平行四边形
, 所以平行四边形 为矩形,又
为矩形,又 ,所以
,所以 ,所以三角形
,所以三角形 为直角三角形,
为直角三角形, .
.
考点:三棱柱,平行六面体的性质,异面直线成角的概念及求法.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
设 是三个互不重合的平面,
是三个互不重合的平面, 是两条不重合的直线,则下列命题中正确的是( )
是两条不重合的直线,则下列命题中正确的是( )
A.若 ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
已知两个不同的平面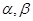 和两条不重合的直线
和两条不重合的直线 ,则下列命题不正确的是 ( )
,则下列命题不正确的是 ( )
A.若  则 则 |
B.若  则 则 |
C.若 , ,  ,则 ,则 |
D.若 , , ,则 ,则 |
设平面 与平面
与平面 相交于直线
相交于直线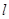 ,直线
,直线 在平面
在平面 内,直线
内,直线 在平面
在平面 内,且
内,且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 是空间的不同直线或不同平面,下列条件中能保证“若
是空间的不同直线或不同平面,下列条件中能保证“若 ,且
,且 ,则
,则 ”为真命题的是 ( )
”为真命题的是 ( )
A.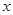 为直线, 为直线,  为平面 为平面 |
B. 为平面 为平面 |
C. 为直线,z为平面 为直线,z为平面 |
D. 为直线 为直线 |
设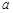 、
、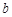 是不同的两条直线,
是不同的两条直线,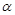 、
、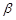 是不同的两个平面,分析下列命题,其中正确的是( ).
是不同的两个平面,分析下列命题,其中正确的是( ).
A.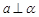 , ,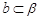 , ,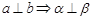 | B.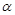 ∥ ∥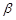 , ,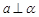 , ,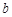 ∥ ∥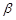 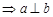 |
C.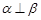 , ,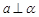 , ,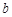 ∥ ∥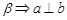 | D.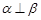 , ,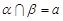 , , |
 ,棱长为1,黑白二蚁都从点
,棱长为1,黑白二蚁都从点 出发,沿棱向前爬行,每走一条棱称为“走完一段”.白蚁爬行的路线是
出发,沿棱向前爬行,每走一条棱称为“走完一段”.白蚁爬行的路线是 黑蚁爬行的路线是
黑蚁爬行的路线是 它们都遵循如下规则:所爬行的第
它们都遵循如下规则:所爬行的第 段所在直线与第
段所在直线与第 段所在直线必须是异面直线(其中
段所在直线必须是异面直线(其中 ).设黑白二蚁走完第2014段后,各停止在正方体的某个顶点处,这时黑白蚁的距离是 ( )
).设黑白二蚁走完第2014段后,各停止在正方体的某个顶点处,这时黑白蚁的距离是 ( )


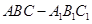 的侧棱与底面垂直,体积为
的侧棱与底面垂直,体积为 ,底面是边长为
,底面是边长为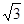 的正三角形,若
的正三角形,若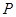 为底面
为底面 的中心,则
的中心,则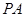 与平面
与平面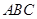 所成角的大小为( )
所成角的大小为( )