题目内容

已知正实数a，b，c满足a+b+c=3，求证：
b
a2
+
c
b2
+
a
c2
≥3．
考点：不等式的基本性质
专题：不等式的解法及应用
分析：利用基本不等式的性质即可得出．
解答： 证明：∵正实数a，b，c满足a+b+c=3，
∴3=a+b+c≥3
3abc
，
∴abc≤1，
∴
b
a2
+
c
b2
+
a
c2
≥3
3
b
a2
•
c
b2
•
a
c2
=3
3
1
abc
≥3．
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
相关题目
已知sin（π+α）=-
3
5
，
5
2
π＜α＜3π，tan（
π
2
-β）=
12
5
，0＜β＜
π
2
，求cos（2α-β）
复数z=（-1+i）2的虚部为（　　）
A、-2B、-2iC、2D、0
某企业为扩大生产规模，今年年初新购置了一条高性能的生产线，该生产线在使用过程中的设备维修、燃料和动力等消耗的费用（称为设备的低劣化值）会逐年增加，第一年设备低劣化值是4万元，从第二年到第七年，每年设备低劣化值均比上年增加2万元，从第八年开始，每年设备低劣化值比上年增加25%．
（1）设第n年该生产线设备低劣化值为an，求an的表达式；
（2）若该生产线前n年设备低劣化平均值为An，当An达到或超过12万元时，则当年需要更新生产线，试判断第几年需要更新该生产线，并说明理由．
设f（x）是一次函数，且∫
1
0
f（x）dx=5，∫
1
0
xf（x）dx=
17
6
，则f（x）的解析式为
 
．
定义域和值域均为[-a，a]（常数a＞0）的函数y=f（x）和y=g（x）的图象如图所示，给出下列四个命题：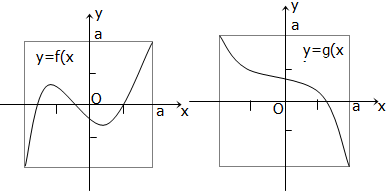
（1）方程f[g（x）]=0有且仅有三个解；
（2）方程g[f（x）]=0有且仅有三个解；
（3）方程f[f（x）]=0有且仅有九个解；
（4）方程g[g（x）]=0有且仅有一个解．
那么，其中正确命题的个数是（　　）
A、（1）（4）
B、（2）（3）
C、（1）（3）
D、（2）（4）
某校100名学生期末考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
（Ⅰ）求图中a的值，并根据频率分布直方图，估计这100名学生数学成绩的平均分；
（Ⅱ）若这100名学生数学成绩在某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如表所示，求语文成绩在[50，90）之外的人数．
分数段[50，60）[60，70）[70，80）[80，90）
x：y5：41：13：55：1
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
3
2
，点P(
3
，
1
2
)在椭圆C上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点Q（2，0），作两条互相垂直的动直线QA、QB，分别交椭圆C于 A、B两点，求证：直线AB必过定点，并求出该定点坐标．
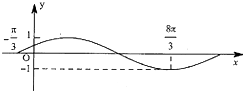将函数y=sinx图象上点的横坐标扩大到原来的m倍，纵坐标保持不变，再向左平移n个单位得到如图所示函数的图象，则m，n可以为（　　）
A、m=2，n=
π
3
B、m=2，n=
11π
3
C、m=4，n=
π
3
D、m=4，n=
11π
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网