题目内容
若sin（| π |
| 2 |
| 3 |
| 5 |
分析：根据两角和的正弦函数公式及特殊角的三角函数值化简后，得到cosθ的值，然后由θ为锐角，利用同角三角函数间的基本关系即可求出sinθ的值．
解答：解：由sin（
+θ）=sin
cosθ+cos
sinθ=cosθ=
，
又θ为锐角，则sinθ=
=
．
故答案为：
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3 |
| 5 |
又θ为锐角，则sinθ=
| 1-cos2θ |
| 4 |
| 5 |
故答案为：
| 4 |
| 5 |
点评：此题考查学生灵活运用两角和的正弦函数公式及同角三角函数间的基本关系化简求值，是一道基础题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
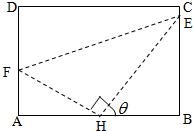如图，某污水处理厂要在一个矩形污水处理池（ABCD）的池底水平铺设污水净化管道（Rt△FHE，H是直角顶点）来处理污水，管道越长，污水净化效果越好．设计要求管道的接口H是AB的中点，E，F分别落在线段BC，AD上．已知AB=20米，