题目内容
矩形ABCD中,AB=20,AD=10
,H是AB中点,E,F分别在边BC和AD上运动,∠EHB=?,∠FHE是直角,
(1)将△EFH的周长L表示成?的函数,并写出定义域
(2)若sinθ+cosθ=
,求L
(3)当取何值时,L最长,求出L的最大值.
| 3 |
(1)将△EFH的周长L表示成?的函数,并写出定义域
(2)若sinθ+cosθ=
| 2 |
(3)当取何值时,L最长,求出L的最大值.
分析:(1)利用三角函数的定义,分别求出FH,EH,EF,进而求得周长及定义域.
(2)利用sinθ+cosθ=
,直接带入即可求L.
(3)设sinθ+cosθ=t,代入L的解析式中,利用θ的范围判断出t的范围,进而求得L的最大值.
(2)利用sinθ+cosθ=
| 2 |
(3)设sinθ+cosθ=t,代入L的解析式中,利用θ的范围判断出t的范围,进而求得L的最大值.
解答:解:(1)∵△EHF是直角三角形,∠BHE=θ,
∴∠AFH=θ,∵AB=2,H是AB中点,
∴AH=FHsinθ=1,FH=
,同理EH=
,EF=
=
∴L=FH+EH+EF=
+
+
=
,当F与D重合时,θ取到最小值
,
当E与C重合时,θ取到最大值
,
∴θ∈[
,
],
∴L=
,θ∈[
,
];
(2)若sinθ+cosθ=
,则平方得1+2sinθcosθ=2,
即sinθcosθ=
,
∴L=
=
=20(
+1).
(3)令sinθ+cosθ=t,则sinθcosθ=
,t=
sin(θ+
)
∴L=
=
=
=
∵θ∈[
,
],
∴θ+
∈[
,
],t=
sin(θ+
)∈[
,
],
∵L=
在[
,
]上单调递减,
∴当t=
,即θ=
时,函数L的最大值为
=20(
+1).

∴∠AFH=θ,∵AB=2,H是AB中点,
∴AH=FHsinθ=1,FH=
| 10 |
| sinθ |
| 10 |
| cosθ |
(
|
| 10 |
| sinθcosθ |
∴L=FH+EH+EF=
| 10 |
| sinθ |
| 10 |
| cosθ |
| 10 |
| sinθcosθ |
| 10(sinθ+cosθ+1) |
| sinθcosθ |
| π |
| 6 |
当E与C重合时,θ取到最大值
| π |
| 3 |
∴θ∈[
| π |
| 6 |
| π |
| 3 |
∴L=
| 10(sinθ+cosθ+1) |
| sinθcosθ |
| π |
| 6 |
| π |
| 3 |
(2)若sinθ+cosθ=
| 2 |
即sinθcosθ=
| 1 |
| 2 |
∴L=
| 10(sinθ+cosθ+1) |
| sinθcosθ |
10(
| ||
|
| 2 |
(3)令sinθ+cosθ=t,则sinθcosθ=
| t2-1 |
| 2 |
| 2 |
| π |
| 4 |
∴L=
| 10(sinθ+cosθ+1) |
| sinθcosθ |
| 10(t+1) | ||
|
| 20(t+1) |
| (t+1)(t-1) |
| 20 |
| t-1 |
∵θ∈[
| π |
| 6 |
| π |
| 3 |
∴θ+
| π |
| 4 |
| 5π |
| 12 |
| 7π |
| 12 |
| 2 |
| π |
| 4 |
| ||||
| 4 |
| 2 |
∵L=
| 20 |
| t-1 |
| ||||
| 4 |
| 2 |
∴当t=
| ||||
| 4 |
| π |
| 6 |
20(3+
| ||
|
| 3 |
点评:本题主要考查了解三角形的实际应用.涉及了通过三角函数的数学模型解决实际问题的问题.综合性较强,难度较大.

练习册系列答案
相关题目
 已知矩形ABCD中,AB=6,BC=6
已知矩形ABCD中,AB=6,BC=6 如图,在矩形ABCD中,
如图,在矩形ABCD中,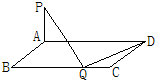 如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于
如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于