题目内容
 如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成600角,则此时B、D的距离是
如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成600角,则此时B、D的距离是
- A.2或

- B.2或

- C.2
- D.1或

B
分析:先利用向量的加法将向量 转化成
转化成  ,等式两边进行平方,求出向量
,等式两边进行平方,求出向量  的模即可.
的模即可.
解答:∵∠ACD=90°,∴ =0.
=0.
同理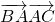 =0.
=0.
∵AB和CD成60°角,∴< >=60°或120°.
>=60°或120°.
∵ ,
,
∴
=3+2×1×1×cos< >
>
=
∴| |=2或
|=2或  ,即B、D间的距离为2或
,即B、D间的距离为2或  .
.
故选B.
点评:本小题主要考查异面直线所成的角,以及数量积表示两个向量的夹角,考查空间想象能力、运算能力和推理论证能力,属于基础题.
分析:先利用向量的加法将向量
 转化成
转化成  ,等式两边进行平方,求出向量
,等式两边进行平方,求出向量  的模即可.
的模即可.解答:∵∠ACD=90°,∴
 =0.
=0.同理
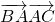 =0.
=0.∵AB和CD成60°角,∴<
 >=60°或120°.
>=60°或120°.∵
 ,
,∴

=3+2×1×1×cos<
 >
>=

∴|
 |=2或
|=2或  ,即B、D间的距离为2或
,即B、D间的距离为2或  .
.故选B.
点评:本小题主要考查异面直线所成的角,以及数量积表示两个向量的夹角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
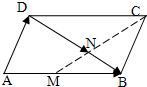 如图,在平行四边形ABCD,
如图,在平行四边形ABCD, 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,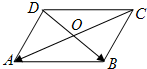 如图,在平行四边形ABCD中,若
如图,在平行四边形ABCD中,若 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.