题目内容
如图，在平行四边形ABCD中，| AB |
| a |
| AD |
| b |
| AN |
| NC |
| BN |
-
+
| 1 |
| 4 |
| a |
| 3 |
| 4 |
| b |
-
+
（用| 1 |
| 4 |
| a |
| 3 |
| 4 |
| b |
| a |
| b |
分析：在△ABN中，利用三角形法则可得
=
+
，利用已知可得
=
，利用平行四边形法则可得
=
+
，代入即可得出．
| BN |
| BA |
| AN |
| AN |
| 3 |
| 4 |
| AC |
| AC |
| AD |
| AB |
解答：解：在△ABN中，
=
+
，
又∵
=
，
=
+
，
∴
=
+
(
+
)
=-
+
=-
+
．
故答案为：-
+
．
| BN |
| BA |
| AN |
又∵
| AN |
| 3 |
| 4 |
| AC |
| AC |
| AD |
| AB |
∴
| BN |
| BA |
| 3 |
| 4 |
| AD |
| AB |
=-
| 1 |
| 4 |
| AB |
| 3 |
| 4 |
| AD |
=-
| 1 |
| 4 |
| a |
| 3 |
| 4 |
| b |
故答案为：-
| 1 |
| 4 |
| a |
| 3 |
| 4 |
| b |
点评：熟练掌握向量的三角形法则和平行四边形法则是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在平行四边形ABCD中，下列结论中错误的是（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
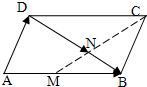如图，在平行四边形ABCD，
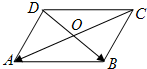如图，在平行四边形ABCD中，若
如图，在平行四边形OABC中，点O是原点，点A和点C的坐标分别是（3，0）、（1，3），点D是线段AB上的中点．