题目内容

10．设抛物线x2=2y的焦点为F，经过点P（1，3）的直线l与抛物线相交于A，B两点，且点P恰为AB的中点，则$|\overrightarrow{AF}|+|\overrightarrow{BF}|$=7．

分析 求出焦点坐标和准线方程，过A、B、P 作准线的垂线段，垂足分别为 M、N、R，利用抛物线的定义得到|AM|+|BN|=2|PR|，求得结果．

解答 解：抛物线 x2=2y的焦点为F（0，0.5），准线方程为y=-0，5，
过A、B、P 作准线的垂线段，
垂足分别为 M、N、R，
点P恰为AB的中点，故|PR|是直角梯形AMNB的中位线，故|AM|+|BN|=2|PR|．
由抛物线的定义可得|AF|+|BF|=|AM|+|BN|=2|PR|=2|3-（-0.5）|=7，
故答案为：7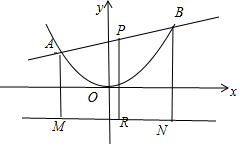

点评 本题考查抛物线的定义、标准方程，以及简单性质的应用，利用抛物线的定义得到|AM|+|BR|=2|PN|，是解题的关键．属于中档题．

练习册系列答案
相关题目
20．如图，某小区准备将闲置的一直角三角形地块开发成公共绿地，图中$∠B=\frac{π}{2}，AB=a，BC=\sqrt{3}a$．设计时要求绿地部分（如图中阴影部分所示）有公共绿地走道MN，且两边是两个关于走道MN对称的三角形（△AMN和△A'MN）．现考虑方便和绿地最大化原则，要求点M与点A，B均不重合，A'落在边BC上且不与端点B，C重合，设∠AMN=θ．
（1）若$θ=\frac{π}{3}$，求此时公共绿地的面积；
（2）为方便小区居民的行走，设计时要求AN，A'N的长度最短，求此时绿地公共走道MN的长度．
1．已知函数f（x）=$\frac{1}{2}{x^2}$-a1nx+b（a，b∈R）．
（Ⅰ）若曲线y=f（x）在x=1处的切线的方程为3x-y-3=0，求实数a，b的值；
（Ⅱ）若-2≤a＜0，对任意x1，x2∈（0，2]，不等式|f（x1）-f（x2）|≤m|$\frac{1}{x_1}-\frac{1}{x_2}$|恒成立，求实数m的最小值．
18．已知抛物线 C：y=$\frac{1}{2}$x2，过不在y轴上的点P作C的两条切线PA，PB，切点分别为A，B．直线AB与y轴交于点 M，直线PO（O为坐标原点）与AB交于点N，且PN⊥AB．
（Ⅰ）证明M是一个定点；
（Ⅱ）求$\frac{|PN|}{|MN|}$的最小值．
5．设F1，F2是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左右焦点，M是C上一点，O是坐标原点，若|MF1|=2|MF2|，|MF2|=|OF2|，则C的离心率是（　　）
A．$\frac{{\sqrt{5}}}{2}$B．$\frac{5}{2}$C．2D．$\sqrt{5}$
15．在△ABC中，a，b，c分别是A，B，C的对边，且$\frac{tanC}{tanB}=-\frac{c}{2a+c}$．
（I）求B；
（II）若b=2$\sqrt{3}$，a+c=4，求△ABC的面积．
2．如图，圆锥的轴截面为三角形SAB，O为底面圆圆心，C为底面圆周上一点，D为BC的中点．
（I）求证：平面SBC⊥平面SOD；
（II）如果∠AOC=∠SDO=60°，BC=2$\sqrt{3}$，求该圆锥的侧面积．
19．执行如图所示的程序框图，输出的i=4．
20．已知命题p：?x＞0，总有（x+1）ex＞1．则￢p为?x0＞0，使得$（{x_0}+1）{e^{x_0}}≤1$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网