题目内容
已知椭圆与双曲线 有相同的焦点,且椭圆过点
有相同的焦点,且椭圆过点 ,
,
(1)求椭圆方程;
(2)直线 过点
过点 交椭圆于
交椭圆于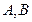 两点,且
两点,且 ,求直线
,求直线 的方程。
的方程。
 有相同的焦点,且椭圆过点
有相同的焦点,且椭圆过点 ,
,(1)求椭圆方程;
(2)直线
 过点
过点 交椭圆于
交椭圆于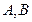 两点,且
两点,且 ,求直线
,求直线 的方程。
的方程。 ;
;
①依题意得,双曲线方程为
∴双曲线两焦点为(0,-1),(0,1)
设所求椭圆方程为
∴
又∵点 在椭圆上
在椭圆上
∴
整理得
解得 ,∴
,∴
∴椭圆方程为
②依题意得M为AB中点,设
直线方程为 ,则
,则
由 ,得
,得
整理得
∵点A、B互异
∴
解得
直线方程为
即

∴双曲线两焦点为(0,-1),(0,1)
设所求椭圆方程为

∴

又∵点
 在椭圆上
在椭圆上∴

整理得

解得
 ,∴
,∴
∴椭圆方程为

②依题意得M为AB中点,设

直线方程为
 ,则
,则
由
 ,得
,得
整理得

∵点A、B互异
∴

解得

直线方程为

即


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 的两条角平分线
的两条角平分线 和
和 相交于H,
相交于H, ,F在
,F在 上,且
上,且 。
。
 。
。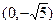 是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为
是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为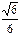 ,椭圆的左右焦点分别为F1和F2 。
,椭圆的左右焦点分别为F1和F2 。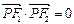 ,若存在,请求出点P的坐标;若不存在,请说明理由。
,若存在,请求出点P的坐标;若不存在,请说明理由。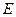 的中心在原点,焦点在
的中心在原点,焦点在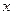 轴上,椭圆上的点到焦点的距离的最小值为
轴上,椭圆上的点到焦点的距离的最小值为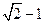 ,离心率为
,离心率为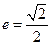 .
.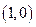 作直线
作直线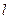 交
交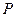 、
、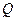 两点,试问:在
两点,试问:在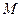 ,使
,使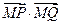 为定值?若存在,求出这个定点
为定值?若存在,求出这个定点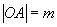 ,求直线
,求直线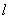 的极坐标方程。
的极坐标方程。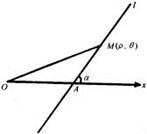
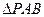 所在的平面
所在的平面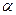 和四边形
和四边形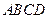 所在的平面
所在的平面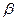 垂直,且
垂直,且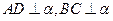 ,
,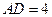 ,
,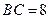 ,
,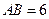 ,
,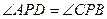 ,则点
,则点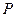 在平面
在平面
 ,
, 距离相等的点的坐标
距离相等的点的坐标 满足的条件.
满足的条件.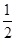 ,m)共线,则实数m=________.
,m)共线,则实数m=________. =1的左焦点F引圆x2 + y2 = 3的切线FP交双曲线右支于点P,T为切点,M为线段FP的中点,O为坐标原点,则| MO | – | MT | 等于 。
=1的左焦点F引圆x2 + y2 = 3的切线FP交双曲线右支于点P,T为切点,M为线段FP的中点,O为坐标原点,则| MO | – | MT | 等于 。