题目内容

函数y=x2+2x+3（x≥0）的值域为
 
．
考点：二次函数的性质
专题：函数的性质及应用
分析：通过求该函数的对称轴即可判断出，x≥0时，该函数的单调性，根据单调性即可求出该函数的值域．
解答： 解：y=x2+2x+3的对称轴为x=-1；
∴该函数在[0，+∞）上为增函数；
若设y=f（x），则f（x）≥f（0）=3；
∴该函数的值域为[3，+∞）．
点评：考查二次函数在某区间上的单调性的判断，以及根据函数单调性求函数的值域．
练习册系列答案
相关题目
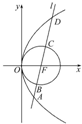如图，抛物线C1：y2=4x和圆C2：（x-1）2+y2=1，直线l经过C1的焦点F，依次交C1，C2于A，B，C，D四点，则
AB
•
CD
的值是
 
．
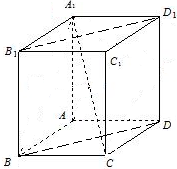已知长方体A1B1C1D1-ABCD的高为
2
，两个底面均为边长1的正方形．
（1）求证：BD∥平面A1B1C1D1；
（2）求异面直线A1C与AD所成角的大小；
（3）求二面角A1-BD-A的平面角的正弦值．
以下四个关于圆锥曲线的命题中：
①A、B为两个定点，k为非零常数，|
PA
|-|
PB
|=k，则动点P的轨迹为双曲线；
②过定圆C上一定点A作圆的动弦AB，P是AB中点，则动点P的轨迹为椭圆；
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
④双曲线
x2
25
-
y2
9
=1与椭圆
x2
35
+y2=1有相同的焦点．其中正确命题的个数（　　）
A、0个B、1个C、2个D、3个
若函数f（x）在定义域D上存在x1，x2，当x1≠x2时
f(x1)-f(x2)
x1-x2
＞0，则称f（x）为“非减函数”．则以下函数是“非减函数”的是
 
．（填上所有正确结论的序号）
①y=1；                   
②y=|2x-1|；
③y=log 
1
2
x+1；
④y=
x-1
x+1
，x∈（0，1）；
⑤y=x 
1
3
，x∈（-2，-1）．
如图，已知矩形ABCD，P为平面ABCD外一点，M、N分别为BC、PD的中点，且满足
MN
=x
.
AB
+y
AD
+z
AP
，则实数x，y，z的值分别为
 
．
已知点P（x0，y0），圆O：x2+y2=r2（r＞O），直线l：x0x+y0y=r2，有以下几个结论：
（1）若点p在圆O上，则直线l与圆O相切；
（2）若点p在圆O外，则直线l与圆O相离；
（3）若点p在圆O内，则直线l与圆O相交；
（4）无论点p在何处，直线l与圆O恒相切．
其中正确的个数是
 
个．
已知函数f（x）是定义域为R，周期为4的奇函数，且当x∈[0，2]时，f（x）=|x-1|-1，则方程f（x）=log4x根的个数为（　　）
A、1B、2C、3D、4
已知函数f（x）=ex-ax-1（a为常数），曲线y=f（x）在与y轴的交点A处的切线斜率为-1．
（Ⅰ）求a的值及函数f（x）的单调区间；
（Ⅱ）证明：当x＞0时，ex＞x2+1；
（Ⅲ）证明：当n∈N*时，1+
1
2
+
1
3
+…+
1
n
＞ln
(n+1)3
(3e)n
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网