题目内容
过P(-2,0)作直线l与圆x2+y2=1交于A,B,若A恰为线段PB的中点,则弦AB的长为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:画出图形,设出AB,利用直角三角形勾股定理,求解即可.
解答:
 解:如图:作OD⊥AB于D,设AB=2t,则PA=2t,
解:如图:作OD⊥AB于D,设AB=2t,则PA=2t,
所以AD2+OD2=1…①,
PD2+OD2=OP2=4…②,
由①得:t2+OD2=1,由②得9t2+OD2=OP2=4,
解得t=
,
弦AB的长为:
.
故答案为:
 解:如图:作OD⊥AB于D,设AB=2t,则PA=2t,
解:如图:作OD⊥AB于D,设AB=2t,则PA=2t,所以AD2+OD2=1…①,
PD2+OD2=OP2=4…②,
由①得:t2+OD2=1,由②得9t2+OD2=OP2=4,
解得t=
| ||
| 4 |
弦AB的长为:
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查直线与圆的位置关系,考查转化思想的应用.

练习册系列答案
相关题目
设集合M={0,1,2},N={x|x2≤x},则M∩N=( )
| A、{0} | B、{1} |
| C、{0,1} | D、{0,1,2} |
有7名大学生志愿者,每人至少会英语和日语中的一种语言,其中会英语的有5人,会日语的有4人,现从中选派2人去担任日语翻译,再选派2人担任英语翻译,则选派方法的种数为( )
| A、37 | B、35 | C、31 | D、28 |
直线l1:(
-1)x+y-2=0与直线l2:x+(
+1)y-3=0的位置关系是( )
| 2 |
| 2 |
| A、平行 | B、相交 | C、垂直 | D、重合 |
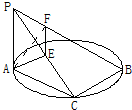 如图PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,E、F分别是点A在PC、PB上的射影,给出下列结论:
如图PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,E、F分别是点A在PC、PB上的射影,给出下列结论: