题目内容
如图,一人在C地看到建筑物A在正北方向,另一建筑物B 在北偏西45°方向,此人向北偏西75°方向前进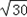 km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.
km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.
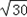 km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.
km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.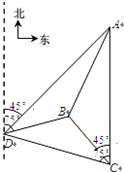
解:依题意得,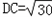 ,∠ADB=∠BCD=30°=∠BDC,
,∠ADB=∠BCD=30°=∠BDC,
∠DBC=120°,∠ADC=60°,∠DAC=45°.
在△BDC中,由正弦定理得,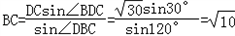 .
.
在△ADC中,由正弦定理得,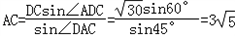 .
.
在△ABC中,由余弦定理得,AB2=AC2+BC2﹣2 AC
AC BC
BC cos∠ACB=
cos∠ACB=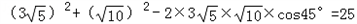 .
.
∴AB=5.
答:这两座建筑物之间的距离为5km.
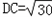 ,∠ADB=∠BCD=30°=∠BDC,
,∠ADB=∠BCD=30°=∠BDC,∠DBC=120°,∠ADC=60°,∠DAC=45°.
在△BDC中,由正弦定理得,
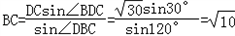 .
.在△ADC中,由正弦定理得,
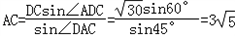 .
.在△ABC中,由余弦定理得,AB2=AC2+BC2﹣2
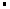 AC
AC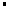 BC
BC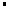 cos∠ACB=
cos∠ACB=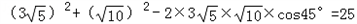 .
.∴AB=5.
答:这两座建筑物之间的距离为5km.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
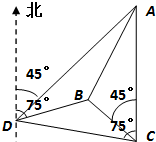 如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进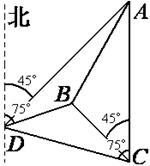
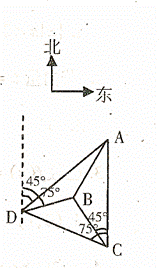
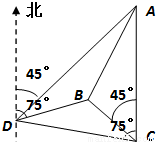 如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进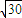 km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.
km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.