题目内容
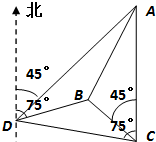 如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进| 6 |
分析:在△ADC中利用正弦定理,结合题意算出AC=3km.然后在△BDC中利用正弦定理得BC=
=
,最后在在△ABC中利用余弦定理加以计算,即可算出AB的长,从而得出两座建筑物A与B之间的距离.
| DCsin∠BDC |
| sin∠DBC |
| 2 |
解答:解:∵在△ADC中,∠ACD=75°,则∠ADC=105°-45°=60°,∠DAC=45°,且CD=
∴由正弦定理,得AC=
=
=3km;…(4分)
又∵在△BDC中,∠BCD=75°-45°=30°,∠BDC=105°-75°=30°,
∴∠DBC=120°,
结合CD=
利用正弦定理,得BC=
=
=
km;…(8分)
在△ABC中,∠ACB=45°,由余弦定理,得AB2=AC2+BC2-2AC•BCcos∠ACB=9+2-6
cos45°=5km2…(12分)
可得AB=
km
答:这两座建筑物A与B之间的距离是
km…(13分)
| 6 |
∴由正弦定理,得AC=
| DCsin∠ADC |
| sin∠DAC |
| ||
| sin45° |
又∵在△BDC中,∠BCD=75°-45°=30°,∠BDC=105°-75°=30°,
∴∠DBC=120°,
结合CD=
| 6 |
| DCsin∠BDC |
| sin∠DBC |
| ||
| sin120° |
| 2 |
在△ABC中,∠ACB=45°,由余弦定理,得AB2=AC2+BC2-2AC•BCcos∠ACB=9+2-6
| 2 |
可得AB=
| 5 |
答:这两座建筑物A与B之间的距离是
| 5 |
点评:本题给出实际应用问题,求两座建筑物之间的距离.着重考查了利用正余弦定理解三角形和解三角形知识在实际生活中的应用,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
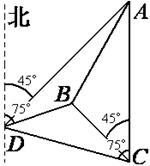
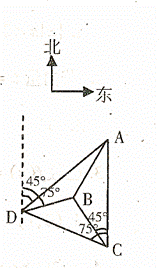
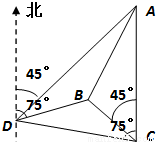 如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进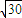 km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.
km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.