题目内容
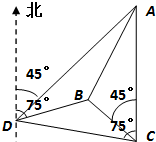 如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进| 30 |
分析:依题意得,DC=
,推出BDC=30°,在△BDC中,在△ADC中,利用正弦定理得,求出BC、AC.在△ABC中,由余弦定理得AB=5.得到结果.
| 30 |
解答:解:依题意得,DC=
,∠ADB=∠BCD=30°=∠BDC,∠DBC=120°,∠ADC=60°,∠DAC=45°.
在△BDC中,由正弦定理得,BC=
=
=
.(6分)
在△ADC中,由正弦定理得,AC=
=
=3
.(9分)
在△ABC中,由余弦定理得,AB2=AC2+BC2-2AC•BCcos∠ACB
=(3
)2+(
)2-2×3
×
×cos45°=25.∴AB=5.
答:这两座建筑物之间的距离为5km.(12分)
| 30 |
在△BDC中,由正弦定理得,BC=
| DCsin∠BDC |
| sin∠DBC |
| ||
| sin120° |
| 10 |
在△ADC中,由正弦定理得,AC=
| DCsin∠ADC |
| sin∠DAC |
| ||
| sin45° |
| 5 |
在△ABC中,由余弦定理得,AB2=AC2+BC2-2AC•BCcos∠ACB
=(3
| 5 |
| 10 |
| 5 |
| 10 |
答:这两座建筑物之间的距离为5km.(12分)
点评:本题是中档题,考查利用正弦定理、余弦定理在实际问题中的应用,注意选择正确的三角形以及合理的定理解答是解好题目的关键,考查计算能力.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
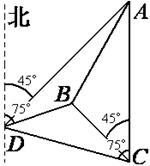
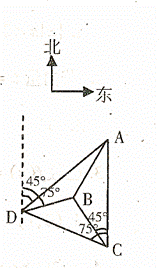
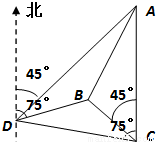 如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进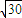 km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.
km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.