题目内容
18．若双曲线$\frac{x^2}{m}-{y^2}=1$的实轴长为4，则此双曲线的渐近线的方程为（ ）| A． | y=±4x | B． | y=±2x | C． | $y=±\frac{1}{2}x$ | D． | $y=±\frac{1}{4}x$ |
分析 由题意可得m=4，求得双曲线的方程，可得渐近线方程为y=±$\frac{1}{2}$x．
解答 解：双曲线$\frac{x^2}{m}-{y^2}=1$的实轴长为4，可得
2$\sqrt{m}$=4，可得m=4，
即有双曲线的方程为$\frac{{x}^{2}}{4}$-y2=1，
可得双曲线的渐近线方程为y=±$\frac{1}{2}$x．
故选：C．
点评 本题考查双曲线的渐近线方程的求法，注意运用双曲线的方程和渐近线方程的关系，考查运算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．函数y=$\sqrt{1-x}$+$\frac{1}{{\sqrt{x}}}$的定义域为（ ）
| A． | {x|0≤x≤1} | B． | {x|x≥0} | C． | {x|x≥1，或x＜0} | D． | {x|0＜x≤1} |
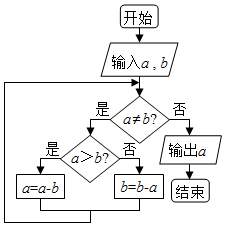如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若在框图中输入的a，b分别为30、18，则输出的a为（ ）