题目内容
 如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.(Ⅰ)求证AE⊥平面BCF;
(Ⅱ)求二面角A-CF-B的平面角的余弦值.
考点:直线与平面垂直的判定,二面角的平面角及求法
专题:空间角,空间向量及应用
分析:(Ⅰ)建立坐标系,利用向量法证明AE⊥平面BCF;
(Ⅱ)求平面的法向量,利用向量法即可求二面角A-CF-B的平面角的余弦值.
(Ⅱ)求平面的法向量,利用向量法即可求二面角A-CF-B的平面角的余弦值.
解答:
证明:(Ⅰ)建立以C1为坐标原点的空间坐标系如图,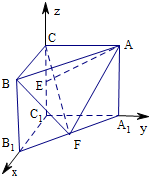
∵AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.
∴A(0,2,2),B(2,0,2),E(0,0,1),A1(0,2,0),F(1,1,0),B1(2,0,0),C(0,0,2)
则
=(0,-2,-1),
=(-2,0,0),
=(1,1,-2),
则
•
=0,
•
=-2+2=0,
则
⊥
,
⊥
,
即AE⊥BC,AE⊥CF,
则AE⊥平面BCF;
(Ⅱ)∵AE⊥平面BCF,
∴
=(0,-2,-1)是平面BCF的法向量,
设平面ACF的法向量为
=(x,y,z),
则
,
解得y=0,x-2z=0,
令z=1,则x=2,即
=(2,0,1),
则cos<
,
>=
=
=
=-
,
则二面角A-CF-B的平面角的余弦值为|cos<
,
>|=
.

∵AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.
∴A(0,2,2),B(2,0,2),E(0,0,1),A1(0,2,0),F(1,1,0),B1(2,0,0),C(0,0,2)
则
| AE |
| BC |
| CF |
则
| AE |
| BC |
| AE |
| CF |
则
| AE |
| BC |
| AE |
| CF |
即AE⊥BC,AE⊥CF,
则AE⊥平面BCF;
(Ⅱ)∵AE⊥平面BCF,
∴
| AE |
设平面ACF的法向量为
| n |
则
|
解得y=0,x-2z=0,
令z=1,则x=2,即
| n |
则cos<
| AE |
| n |
| ||||
|
|
| -1 | ||||
|
| -1 | ||||
|
| 1 |
| 5 |
则二面角A-CF-B的平面角的余弦值为|cos<
| AE |
| n |
| 1 |
| 5 |
点评:本题主要考查空间直线和平面垂直的判断已经空间二面角的求解,建立坐标系利用向量法是解决本题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
某几何体的三视图的形状和尺寸如图所示,则其体积是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
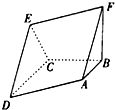 如图空间几何体ABCDEF中,四边形ADEF为平行四边形,FB⊥平面ABCD,AB∥CD,AB⊥BC,AB=BC=
如图空间几何体ABCDEF中,四边形ADEF为平行四边形,FB⊥平面ABCD,AB∥CD,AB⊥BC,AB=BC= 已知函数f(x)=2
已知函数f(x)=2