题目内容
14.若复数z满足z+z•i=2+3i,则在复平面内z对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由z+z•i=2+3i,得$z=\frac{2+3i}{1+i}$,然后利用复数代数形式的乘除运算化简,求出在复平面内z对应的点的坐标,则答案可求.
解答 解:由z+z•i=2+3i,
得$z=\frac{2+3i}{1+i}$=$\frac{(2+3i)(1-i)}{(1+i)(1-i)}=\frac{5+i}{2}=\frac{5}{2}+\frac{1}{2}i$,
则在复平面内z对应的点的坐标为:($\frac{5}{2}$,$\frac{1}{2}$),位于第一象限.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
19.已知条件p:|x+1|<2,条件q:3x<3,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.已知A,B,P是双曲线mx2-ny2=1(m>0,n>0)上不同的三点,且A,B连线经过坐标原点,若直线PA,PB的斜率积为$\frac{2}{3}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |

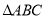 和
和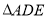 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形, ,点
,点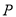 为射线
为射线 与射线
与射线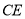 的交点.
的交点.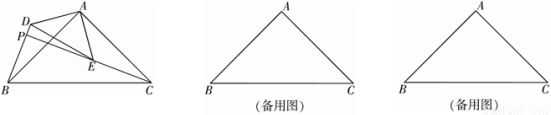
 ;
; ,把
,把 绕点
绕点 旋转,
旋转, 时,求
时,求 的长;
的长;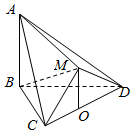 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.