题目内容
3.已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)和曲线C2:$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{3}$=1有相同的焦点,曲线C1的离心率是曲线C2的离心率的$\sqrt{5}$倍.(Ⅰ)求曲线C1的方程;
(Ⅱ)设点A是曲线C1的右支上一点,F为右焦点,连AF交曲线C1的右支于点B,作BC垂直于定直线l:x=$\frac{\sqrt{2}}{2}$,垂足为C,求证:直线AC恒过x轴上一定点.
分析 (Ⅰ)由题知:a2+b2=2,曲线C2的离心率为$\frac{\sqrt{2}}{\sqrt{5}}$,利用曲线C1的离心率是曲线C2的离心率的$\sqrt{5}$倍,求出a,b,即可求曲线C1的方程;
(Ⅱ)由于研究直线恒过定点,求出AC的方程,令y=0,求出x可得(x与直线AB斜率k无关),可证直线AC恒过定点就可解决.
解答 (Ⅰ)解:由题知:a2+b2=2,曲线C2的离心率为$\frac{\sqrt{2}}{\sqrt{5}}$…(2分)
∵曲线C1的离心率是曲线C2的离心率的$\sqrt{5}$倍,
∴$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$=$\sqrt{5}×\frac{\sqrt{2}}{\sqrt{5}}$即a2=b2,…(3分)
∴a=b=1,∴曲线C1的方程为x2-y2=1; …(4分)
(Ⅱ)证明:由直线AB的斜率不能为零知可设直线AB的方程为:x=ny+$\sqrt{2}$ …(5分)
与双曲线方程x2-y2=1联立,可得(n2-1)y2+2$\sqrt{2}$ny+1=0
设A(x1,y1),B(x2,y2),则y1+y2=-$\frac{2\sqrt{2}n}{{n}^{2}-1}$,y1y2=$\frac{1}{{n}^{2}-1}$,…(7分)
由题可设点C($\frac{\sqrt{2}}{2}$,y2),
由点斜式得直线AC的方程:y-y2=$\frac{{y}_{2}-{y}_{1}}{\frac{\sqrt{2}}{2}-{x}_{1}}$(x-$\frac{\sqrt{2}}{2}$) …(9分)
令y=0,可得x=$\frac{-\frac{\sqrt{2}}{2}{y}_{2}+{y}_{2}{x}_{1}}{{y}_{2}-{y}_{1}}$=$\frac{-3n-\frac{3\sqrt{2}}{2}{y}_{1}(1-{n}^{2})}{-2\sqrt{2}n-2{y}_{1}(1-{n}^{2})}$=$\frac{3\sqrt{2}}{4}$ …(11分)
∴直线AC过定点($\frac{3\sqrt{2}}{4}$,0). …(12分)
点评 本题考查双曲线的方程与性质,考查直线恒过定点,考查学生分析解决问题的能力,属于中档题.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | a>0 | B. | a≥0 | C. | a<0 | D. | a≤0 |
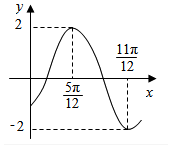
| A. | $-\frac{3}{2}$ | B. | -1 | C. | $-\sqrt{2}$ | D. | $-\sqrt{3}$ |
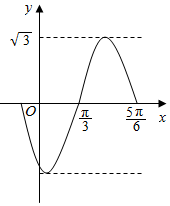 已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{2π}{3}$)(ω>0)的部分图象如图所示,则函数g(x)=cos(ωx+$\frac{2π}{3}$)的图象的一条对称轴方程为( )
已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{2π}{3}$)(ω>0)的部分图象如图所示,则函数g(x)=cos(ωx+$\frac{2π}{3}$)的图象的一条对称轴方程为( )| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |