题目内容
10.已知A是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左顶点,F1,F2分别为双曲线的左、右焦点,P为双曲线上一点,G是△PF1F2的重心,若$\overrightarrow{GA}$=λ$\overrightarrow{P{F}_{1}}$,则双曲线的渐近线方程为( )| A. | $y=±\sqrt{3}x$ | B. | $y=±2\sqrt{2}x$ | C. | $y=±\frac{{\sqrt{5}}}{2}x$ | D. | 与λ的取值有关 |
分析 由题意,PG=2GO,GA∥PF1,可得2OA=AF1,即可求出双曲线的渐近线方程.
解答 解:由题意,PG=2GO,GA∥PF1,
∴2OA=AF1,
∴2a=c-a,∴c=3a,
∴b=2$\sqrt{2}$a,
∴双曲线的渐近线方程为y=±2$\sqrt{2}$x.
故选:B.
点评 本题考查双曲线的渐近线方程,考查学生的计算能力,比较基础.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
5.设集合A={0,1,2,4},B=$\left\{{\left.{x∈R|\frac{x-4}{x-2}≤0}\right\}}$,则A∩B=( )
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {4} | D. | {x|1<x≤4} |
15.已知双曲线的焦距为2$\sqrt{3}$,焦点到一条渐近线的距离为$\sqrt{2}$,则双曲线的标准方程为( )
| A. | x2-$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | ||
| C. | x2-$\frac{{y}^{2}}{2}$=1或y2-$\frac{{x}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-y2=1或$\frac{{y}^{2}}{2}$-x2=1 |
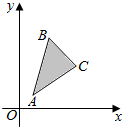 给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3)若使目标函数z=ax-y仅在点C处取得最大值,则a的取值范围是$({\frac{2}{3},+∞})$.
给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3)若使目标函数z=ax-y仅在点C处取得最大值,则a的取值范围是$({\frac{2}{3},+∞})$. 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100]
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100]