题目内容
2.已知直线过点M(-3,0),且倾斜角为30°,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左焦点为F1(-2,0),离心率$e=\frac{{\sqrt{6}}}{3}$.(Ⅰ)求直线l和椭圆C的方程;
(Ⅱ)求证:直线l和椭圆C有两个交点;
(Ⅲ)设直线l和椭圆C的两个交点为A,B,求证:以线段AB为直径的圆经过点F1.
分析 (Ⅰ)由直线l倾斜角为30°,直线l过点M(-3,0),能求出直线l的方程;由椭圆的焦点坐标和离心率求出a,b,由此能求出椭圆C的方程.
(Ⅱ)直线与椭圆联立,得2x2+6x+3=0.由此利用根的判别式能证明直线l和椭圆C有两个交点.
(Ⅲ)设A(x1,y1),B(x2,y2),由韦达定理推导出F1A⊥F1B,由此能证明以线段AB为直径的圆经过点F1.
解答 (本小题满分14分)
解:(Ⅰ)由直线l倾斜角为30°,
知直线l的斜率为$\frac{\sqrt{3}}{3}$,又直线l过点M(-3,0),
得直线l的方程为y=$\frac{\sqrt{3}}{3}$(x+3),即x-$\sqrt{3}y+3$=0.
∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左焦点为F1(-2,0),离心率$e=\frac{{\sqrt{6}}}{3}$,
∴由题意知,c=2,e=$\frac{c}{a}=\frac{\sqrt{6}}{3}$,得a=$\sqrt{6}$,
∴b2=6-4=2,
∴椭圆C的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$.(5分)
证明:(Ⅱ)由方程组$\left\{\begin{array}{l}{{x}^{2}+3{y}^{2}=6}\\{y=\frac{\sqrt{3}}{3}(x+3)}\end{array}\right.$,得2x2+6x+3=0.
△=62-4×2×3=12>0,
∴直线l和椭圆C有两个交点.(10分)
(Ⅲ)设A(x1,y1),B(x2,y2),则x1+x2=-3,${x}_{1}{x}_{2}=\frac{3}{2}$.
∵${k}_{{F}_{1}A}•{k}_{{F}_{1}B}$=$\frac{{y}_{1}}{{x}_{1}+2}•\frac{{y}_{2}}{{x}_{2}+2}$=$\frac{\frac{1}{3}({x}_{1}+3)({x}_{2}+3)}{({x}_{1}+2)({x}_{2}+2)}$=$\frac{{x}_{1}{x}_{2}+3({x}_{1}+{x}_{2})+9}{3[{x}_{1}{x}_{2}+2({x}_{1}+{x}_{2})+4]}$=-1,
∴F1A⊥F1B,
∴以线段AB为直径的圆经过点F1.(14分)
点评 本题考查椭圆方程的求法,考查直线与椭圆有两个交点的证明,考查以线段AB为直径的圆经过点F1的证明,是中档题,解题时要认真审题,注意根的判别式、韦达定理、直线方程等知识点的合理运用.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| x | 2 | 3 | 4 | 5 |
| y | 1.5 | 2 | 3 | 3.5 |
(2)已知该厂技改前100吨甲产品的生产能耗为85吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.$.
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{8}{3}$ | D. | 4 |
高一:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
高二:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(Ⅰ)根据两组数据完成两个年级满意度评分的茎叶图,并通过茎叶图比较两个年级满意度评分的平均值及离散程度(不要求计算出具体值,给出结论即可);
| 高一 | 茎 | 高二 | ||||||||||
| 4 | ||||||||||||
| 3 | 5 | |||||||||||
| 6 | 4 | 2 | 6 | |||||||||
| 6 | 8 | 8 | 6 | 4 | 3 | 7 | ||||||
| 9 | 2 | 8 | 6 | 5 | 1 | 8 | ||||||
| 7 | 5 | 5 | 2 | 9 | ||||||||
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
| A. | 8 | B. | 13 | C. | 14 | D. | 20 |
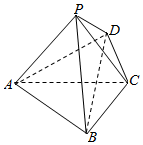 如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,$∠ACB=∠ACD=\frac{π}{3}$
如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,$∠ACB=∠ACD=\frac{π}{3}$