题目内容
14.设椭圆M的方程为:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1.(1)求M的长轴长与短轴长;
(2)若椭圆N的焦点为椭圆M在y轴上的顶点,且椭圆N经过点A(-$\sqrt{2}$,$\frac{3\sqrt{2}}{2}$),求椭圆N的方程.
分析 (1)求出椭圆M的a,b,即可得到长轴长2a,短轴长2b;
(2)求出椭圆M的短轴的顶点,可设椭圆N的方程为$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0),由焦点坐标和A点满足椭圆方程,解方程可得所求.
解答 解:(1)椭圆M的方程为:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的a=3,b=$\sqrt{5}$,
可得M的长轴长为6,短轴长为2$\sqrt{5}$;
(2)由椭圆M可得y轴上的顶点为(0,±$\sqrt{5}$),
设椭圆N的方程为$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0),
由题意可得,m2-n2=5,
$\frac{9}{2{m}^{2}}$+$\frac{2}{{n}^{2}}$=1,
解得m=3,n=2,
即有椭圆N的方程为$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1.
点评 本题考查椭圆的方程和性质,注意求出椭圆的基本元素,考查方程的思想的运用,属于基础题.

练习册系列答案
相关题目
4.设f(x)=xex的导函数为f′(x),则f′(1)的值为( )
| A. | e | B. | e+1 | C. | 2e | D. | e+2 |
9.已知函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,则f($\frac{5π}{6}$)=( )
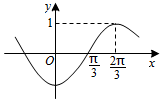

| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
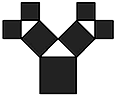 如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.
如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.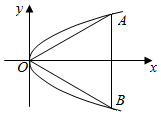 如图,等边三角形OAB的边长为8$\sqrt{3}$,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点.
如图,等边三角形OAB的边长为8$\sqrt{3}$,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点.