题目内容
4.在正方形ABCD中,AB=AD=2,M,N分别为边BC,CD上的两个动点且MN=$\sqrt{2}$,则$\overline{AM}$•$\overline{AN}$的取值范围为( )| A. | [4,8-2$\sqrt{2}$] | B. | [4-2$\sqrt{2}$,8] | C. | [4,8+2$\sqrt{2}$] | D. | [4-2$\sqrt{2}$,8-2$\sqrt{2}$] |
分析 如图所示,设M(2,y),N(x,2),$(2-\sqrt{2}≤x≤2,2-\sqrt{2}≤y≤2)$.由于MN=$\sqrt{2}$,可得(x-2)2+(y-2)2=2.则$\overline{AM}$•$\overline{AN}$=2x+2y=t,数形结合即可得出.
解答 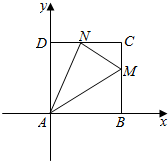 解:如图所示,
解:如图所示,
设M(2,y),N(x,2),$(2-\sqrt{2}≤x≤2,2-\sqrt{2}≤y≤2)$.
∵MN=$\sqrt{2}$,
∴$\sqrt{(x-2)^{2}+(y-2)^{2}}$=$\sqrt{2}$,化为(x-2)2+(y-2)2=2.
则$\overline{AM}$•$\overline{AN}$=2x+2y=t,
由$\frac{|4+4-t|}{\sqrt{8}}$=$\sqrt{2}$,解得t=4或12(舍去).
把x=2$-\sqrt{2}$,y=2代入可得t=8-2$\sqrt{2}$.
综上可得:t∈$[4,8-2\sqrt{2}]$.
故选:A.
点评 本题考查了数量积运算性质、两点之间的距离公式、直线与圆相切相交性质、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.某人向正东方向走2$\sqrt{3}$千米后,再沿北偏西60°方向走了3千米,结果他离出发点恰好x千米,那么x的值为( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{21-6\sqrt{3}}$ | D. | 3 |
12.若直线l1:ax+2y+6=0与直线l2:x+(a-1)y+(a2-1)=0平行而不重合,则a等于( )
| A. | -1或2 | B. | -1 | C. | 2 | D. | $\frac{2}{3}$ |
14.在空间直角坐标系Oxy中,$\overrightarrow{AB}=-\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}}-3\overrightarrow{{e}_{3}}$($\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}},\overrightarrow{{e}_{3}}$)分别是与x轴、y轴、z轴的正方向同向的单位向量),则点B的坐标为( )
| A. | (-$\overrightarrow{{e}_{1}},2\overrightarrow{{e}_{2}},-3\overrightarrow{{e}_{3}}$) | B. | (-1,2,-3) | C. | (1,-2,3) | D. | 不能确定 |
 如图,M为曲线y=-$\frac{4}{x}$上的一点.过点M作x轴、y轴的垂线.垂足分别为E、F.分别交直线y=$\frac{\sqrt{3}}{3}$x+m于点D、C两点.若直线y=$\frac{\sqrt{3}}{3}$x+m与y轴交于点A.与x轴相交于点B;
如图,M为曲线y=-$\frac{4}{x}$上的一点.过点M作x轴、y轴的垂线.垂足分别为E、F.分别交直线y=$\frac{\sqrt{3}}{3}$x+m于点D、C两点.若直线y=$\frac{\sqrt{3}}{3}$x+m与y轴交于点A.与x轴相交于点B;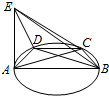 已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).
已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).