题目内容
9.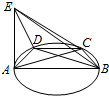 已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).
已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).(1)求证:△BCE为直径三角形;
(2)若四边形ABCE为一个等腰梯形,且BC=1,求几何体C-BDE的体积.
分析 (1)证明BC⊥平面ACE,可得BC⊥EC,从而△BCE为直角三角形;
(2)几何体C-BDE的体积=几何体E-BCD的体积,利用体积公式可得结论.
解答 (1)证明:由题意,AE⊥平面ABD,则AE⊥BC,
∵AB为直径,∴AC⊥BC,
∵AC∩AE=A,
∴BC⊥平面ACE,
∴BC⊥EC,
∴△BCE为直角三角形;
(2)解:由∠ABD=$\frac{π}{6}$,四边形ABCD为一个等腰梯形,且BC=1,可得DC=1,∠BCD=120°,
∴S△BCD=$\frac{1}{2}×1×1×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,
∵AE=AB=2
∴几何体C-BDE的体积=几何体E-BCD的体积=$\frac{1}{3}×\frac{\sqrt{3}}{4}×2$=$\frac{\sqrt{3}}{6}$.
点评 本题考查线面垂直的判定,考查几何体体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
20.一个与正四棱锥的底面平行的平面把正四棱锥截成两部分,一部分是棱锥,一部分是棱台,已知被截得的棱台的上、下底面的边长分别是方程x2-6x+8=0的两根,且截得的棱台的侧面积等于此棱台上、下底面面积之和,则该四校锥的高为( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
4.在正方形ABCD中,AB=AD=2,M,N分别为边BC,CD上的两个动点且MN=$\sqrt{2}$,则$\overline{AM}$•$\overline{AN}$的取值范围为( )
| A. | [4,8-2$\sqrt{2}$] | B. | [4-2$\sqrt{2}$,8] | C. | [4,8+2$\sqrt{2}$] | D. | [4-2$\sqrt{2}$,8-2$\sqrt{2}$] |
14.长方体ABCD-A1B1C1D1中,E、F分别为线段AA1、B1C上的点,若AB=6,BC=5.AA1=3.则三棱锥D1-EDF的体积为( )
| A. | $\frac{15}{2}$ | B. | 15 | ||
| C. | 30 | D. | 随点E、F的改变而改变的值 |