题目内容
5.已知p:m∈(-2,-1),q:m满足$\frac{x^2}{2+m}-\frac{y^2}{m+1}=1$表示椭圆,那么p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 由已知列关于m的不等式组,求解m的范围,结合必要条件、充分条件及充要条件的判断方法得答案.
解答 解:由$\frac{x^2}{2+m}-\frac{y^2}{m+1}=1$表示椭圆,
得$\left\{\begin{array}{l}{2+m>0}\\{m+1<0}\\{2+m≠-m-1}\end{array}\right.$,解得-2<m<-1且m$≠-\frac{3}{2}$.
∴p是q的必要不充分条件.
故选:B.
点评 本题考查必要条件、充分条件及充要条件的判断方法,考查了椭圆的标准方程,是基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
19.一辆汽车在司机猛踩刹车后5s内停下.在这一刹车过程中,下面各速度值被记录了下来:
求刹车踩下后汽车滑过的距离的不足近似值(每个ξi均取为小区间的右端点)与过剩近似值(每个ξi均取为小区间的左端点).
| 刹车踩下后的时间/s | 0 | 1 | 2 | 3 | 4 | 5 |
| 速度/(m•s-1) | 27 | 18 | 12 | 7 | 3 | 0 |
20.设P是△ABC所在平面内的一点,且$\overrightarrow{CP}$=2$\overrightarrow{PA}$,则△PAB与△PBC的面积之比是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
17.已知i是虚数单位,复数$\frac{5}{1-i}$=( )
| A. | i-2 | B. | $\frac{5}{2}$+$\frac{i}{2}$ | C. | -2 | D. | 2 |
14.已知函数f(x)=lgx,若f(a-1)+f(b-1)=0且a>1,b>1,则a+b的取值范围( )
| A. | [4,+∞) | B. | (4,+∞) | C. | (0,$\frac{1}{4}$] | D. | [2,+∞) |
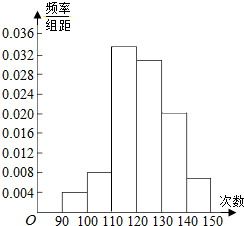 为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.
为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.