题目内容
4.求下列三角函数值:(1)sin$\frac{4π}{3}$•cos$\frac{25π}{6}$•tan$\frac{5π}{4}$;
(2)sin[(2n+1)π-$\frac{2π}{3}$].
分析 直接利用诱导公式对(1)(2)化简求值.
解答 解:(1)sin$\frac{4π}{3}$•cos$\frac{25π}{6}$•tan$\frac{5π}{4}$=$-sin\frac{π}{3}•cos\frac{π}{6}•tan\frac{π}{4}$=-$\frac{\sqrt{3}}{2}•\frac{\sqrt{3}}{2}•1=-\frac{3}{4}$;
(2)sin[(2n+1)π-$\frac{2π}{3}$]=sin(2n$π+\frac{π}{3}$)=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查三角函数的化简求值,考查诱导公式的应用,是基础的计算题.

练习册系列答案
相关题目
9.已知点M(3,y0)是抛物线y2=2px(0<p<6)上一点,且M到抛物线焦点的距离是M到直线$x=\frac{p}{2}$的距离的2倍,则p等于( )
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
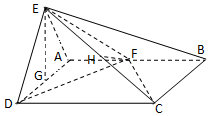 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.