题目内容
11.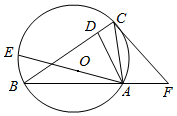 如图,AE是⊙O的直径,△ABC内接于⊙O,AB=BC,AD⊥BC,垂足为D.
如图,AE是⊙O的直径,△ABC内接于⊙O,AB=BC,AD⊥BC,垂足为D.(Ⅰ)求证:AE•AD=AC•BC;
(Ⅱ)过点C作⊙O的切线交BA的延长线于F,若AF=4,CF=6,求AC的长.
分析 (Ⅰ)连接BE,由直径所对圆周角为直角得到∠ABE=90°,由三角形相似的条件得到△ACD∽△AEB,再由相似三角形对应边成比例得AE•AD=AC•BC;
(Ⅱ)由切割弦定理可得CF2=AF•BF,然后再由三角形相似求得AC的值.
解答 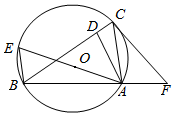 (Ⅰ)证明:连接BE
(Ⅰ)证明:连接BE
∵AE为圆O的直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ABE=∠ADC,
又∵∠ACD=∠AEB,
∴△ACD∽△AEB,
∴$\frac{AD}{AB}=\frac{AC}{AE}$,
又∵AB=BC,
∴AE•ED=AC•BC;
(Ⅱ)解:∵CF是圆O的切线,
∴CF2=AF•BF,
又AF=4,CF=6,
∴BF=9,
∴AB=BF-AF=5,
又∵∠ACF=∠FBC,∠F为公共角,
∴△AFC∽△CFB,
∴$\frac{AF}{CF}=\frac{AC}{CB}$,
∴AC=$\frac{AF•CB}{CF}=\frac{10}{3}$.
点评 本题考查与线段有关的比例线段,考查相似三角形的应用,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
10.已知向量的集合A={$\overrightarrow{m}$|$\overrightarrow{m}$=(x,y),x2+y2≤1}中的任意两个向量$\overrightarrow{{m}_{1}}$,$\overrightarrow{{m}_{2}}$与两个非负实数a,b,那么|a$\overrightarrow{{m}_{1}}$+b$\overrightarrow{{m}_{2}}$|与a+b的关系为( )
| A. | |a$\overrightarrow{{m}_{1}}$+b$\overrightarrow{{m}_{2}}$|>a+b | B. | |a$\overrightarrow{{m}_{1}}$+b$\overrightarrow{{m}_{2}}$|≤a+b | C. | |a$\overrightarrow{{m}_{1}}$+b$\overrightarrow{{m}_{2}}$|≥a+b | D. | |a$\overrightarrow{{m}_{1}}$+b$\overrightarrow{{m}_{2}}$|<a+b |
11.若直线mx-y-1=0与直线x-2y+3=0垂直,则m的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
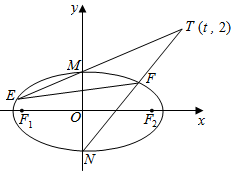 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为$\sqrt{3}$,又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的上顶点M与左、右焦点F1,F2构成三角形MF1F2面积为$\sqrt{3}$,又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$.