题目内容
过点P(1,2)的直线l与x轴、y轴正半轴分别交于A、B两点.
(Ⅰ)若P为AB中点时,求的方程;
(Ⅱ)若|OA|+|OB|最小时,求△AOB的面积S.
(Ⅰ)若P为AB中点时,求的方程;
(Ⅱ)若|OA|+|OB|最小时,求△AOB的面积S.
考点:直线的截距式方程
专题:直线与圆
分析:(Ⅰ)由中点坐标公式求出A,B的坐标,直接由截距式方程得答案;
(Ⅱ)设出直线方程的截距式,代入点的坐标,得到
+
=1,由基本不等式求出|OA|+|OB|取最小时得a,b的值,代入三角形面积公式得答案.
(Ⅱ)设出直线方程的截距式,代入点的坐标,得到
| 1 |
| a |
| 2 |
| b |
解答:
解:(Ⅰ)设A(a,0),B(0,b),
∵P(1,2)为AB的中点,
∴A(2,0),B(0,4),
∴由截距式得
+
=1,
即的方程为2x+y-4=0;
(Ⅱ)依题得直线l与x轴不垂直,设A(a,0),B(0,b)(a>0,b>0),
∴
+
=1,
又直线l过点P(1,2),
∴
+
=1,
∴|OA|+|OB|=a+b=(a+b)•(
+
)=3+
+
≥3+2
=3+2
.
当且仅当
=
时取等号,此时a=
+1,b=2+
.
∴当a=
+1,b=2+
时,|OA|+|OB|取最小值.
∴S=
ab=
(
+1)•(2+
)=
.
∵P(1,2)为AB的中点,
∴A(2,0),B(0,4),
∴由截距式得
| x |
| 2 |
| y |
| 4 |
即的方程为2x+y-4=0;
(Ⅱ)依题得直线l与x轴不垂直,设A(a,0),B(0,b)(a>0,b>0),
∴
| x |
| a |
| y |
| b |
又直线l过点P(1,2),
∴
| 1 |
| a |
| 2 |
| b |
∴|OA|+|OB|=a+b=(a+b)•(
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 2a |
| b |
|
| 2 |
当且仅当
| b |
| a |
| 2a |
| b |
| 2 |
| 2 |
∴当a=
| 2 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
4+3
| ||
| 2 |
点评:本题考查了直线方程的截距式,训练了利用基本不等式求最值,关键是对“1”的灵活运用,是中档题.

练习册系列答案
相关题目
若双曲线
-
=1的离心率为2,则实数m的值为( )
| x2 |
| 2 |
| y2 |
| m |
A、2
| ||
| B、3 | ||
C、
| ||
| D、6 |
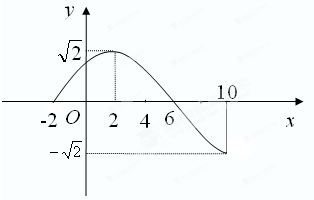 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<