题目内容
已知三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1⊥面ABC,高为5,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为 .
考点:多面体和旋转体表面上的最短距离问题
专题:计算题,空间位置关系与距离
分析:将三棱柱展开两次如图,不难发现最短距离是六个矩形对角线的连线,正好相当于绕三棱柱转两次的最短路径.
解答:
解:将正三棱柱ABC-A1B1C1沿侧棱展开,再拼接一次,其侧面展开图如图所示,
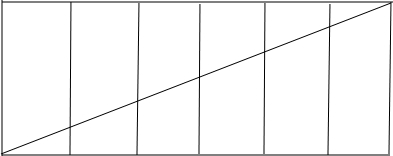
在展开图中,最短距离是六个矩形对角线的连线的长度,也即为三棱柱的侧面上所求距离的最小值.
由已知求得矩形的长等于6×2=12,宽等于5,由勾股定理d=
=13
故答案为:13.

在展开图中,最短距离是六个矩形对角线的连线的长度,也即为三棱柱的侧面上所求距离的最小值.
由已知求得矩形的长等于6×2=12,宽等于5,由勾股定理d=
| 122+52 |
故答案为:13.
点评:本题考查棱柱的结构特征,空间想象能力,几何体的展开与折叠,体现了转化(空间问题转化为平面问题,化曲为直)的思想方法.

练习册系列答案
相关题目