题目内容
9.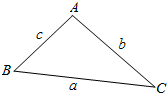 (1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
(1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.(2)已知在Rt△ABC中.AB⊥AC,AD⊥BC于D,有$\frac{1}{AD^2}$=$\frac{1}{AB^2}$+$\frac{1}{AC^2}$成立.那么在四面体A一BCD中,类比上述结论,你能得怎样的猜想,说明猜想是否正确并给出理由.
分析 (1)这是一个升维类比,线类比为面,线线角类比为面面角.
(2)利用平面中的射影定理证明;将平面中的三角形类比成空间的三棱锥,三角形的两边垂直类比成三棱锥的三棱垂直,得到类比性质通过作辅助线将空间的证明问题转化为三角形中的性质.
解答 解:(1)如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推理到三维空间,其表现形式应为S=S1cosα+S2cosβ+S3cosγ,
(2):类比AB⊥AC,AD⊥BC猜想:在四面体ABCD中,若AB⊥AC,AB⊥AD,AC⊥AD,AE⊥平面BCD,则$\frac{1}{A{E}^{2}}$=$\frac{1}{A{B}^{2}}$+$\frac{1}{A{C}^{2}}$+$\frac{1}{A{D}^{2}}$.
如图,连接BE交CD于F,连接AF.
∵AB⊥AC,AB⊥AD
∴AB⊥平面ACD.
而AF?平面ACD,∴AB⊥AF.
在Rt△ABF中,AE⊥BF,
∴$\frac{1}{A{E}^{2}}$=$\frac{1}{A{B}^{2}}$+$\frac{1}{A{F}^{2}}$.
在Rt△ACD中,AF⊥CD,
∴$\frac{1}{A{F}^{2}}$=$\frac{1}{A{C}^{2}}$+$\frac{1}{A{D}^{2}}$.
∴则$\frac{1}{A{E}^{2}}$=$\frac{1}{A{B}^{2}}$+$\frac{1}{A{C}^{2}}$+$\frac{1}{A{D}^{2}}$,
故猜想成立.
点评 本题考查利用类比推理得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论.

 阅读快车系列答案
阅读快车系列答案| 性别 是否需要志愿者 | 男 | 女 | 总计 |
| 需要 | 30 | ||
| 不需要 | 160 | ||
| 总计 | 200 | 500 |
(Ⅱ)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关.
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | f(a)+f(b)<2f(1) | B. | f(a)+f(b)≤2f(1) | C. | f(a)+f(b)≥2f(1) | D. | f(a)+f(b)>2f(1) |
| A. | 4 | B. | $\frac{14}{3}$ | C. | $\frac{16}{3}$ | D. | 6 |
| A. | [$\frac{1}{2}$,17] | B. | [1,17] | C. | [1,$\sqrt{17}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{17}$] |
 如图,有一个底面半径与高均为4米的圆锥形水池装满了水,现要把它抽干(即水全部抽出),问需用功多少?(水的比重ρ=1)
如图,有一个底面半径与高均为4米的圆锥形水池装满了水,现要把它抽干(即水全部抽出),问需用功多少?(水的比重ρ=1)